题目内容
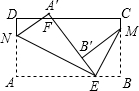
 如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角是
∠B′EM,∠MEB,∠A′NE
∠B′EM,∠MEB,∠A′NE
(只需填写三个角).分析:由折叠的性质得到∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,再由平角的定义得到NE与ME垂直,根据同角(等角)的余角相等,即可在图中找出与∠B′ME互余的角.
解答:解:由折叠及长方形ABCD可得:∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,
∵∠MEB+∠MEB′+∠AEN+∠A′EN=180°,
∴∠MEB+∠AEN=∠MEB′+∠A′EN=90°,
则图中与∠B′ME互余的角是∠B′EM,∠MEB,∠A′NE.
故答案为:∠B′EM,∠MEB,∠A′NE.
∵∠MEB+∠MEB′+∠AEN+∠A′EN=180°,
∴∠MEB+∠AEN=∠MEB′+∠A′EN=90°,
则图中与∠B′ME互余的角是∠B′EM,∠MEB,∠A′NE.
故答案为:∠B′EM,∠MEB,∠A′NE.
点评:此题考查了余角和补角,以及翻折变换,熟练掌握图形折叠的性质是解本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为( )
如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为( ) 如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为
如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为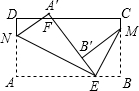 如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互