题目内容

从边长相等的正三角形、正四边形、正五边形、正六边形、正八边形中任选两种不同的正多边形，能够进行平面镶嵌的概率是 （  ）           
A．B．C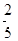．D．
B
分别用A、B、C、D、E 表示正三角形、正四边形、正五边形、正六边形、正八边形，列表如下：
第一次
第二次
A
B
C
D
E
A
 
B A
C A
DA
EA
B
A B
 
CB
DB
EB
C
AC
BC
 
DC
EC
D
AD
BD
CD
 
ED
E
AE
BE
CE
DE
 
由列表可以看出，所有可能结果共有20个，能镶嵌成一个平面图案（记为事件G）的有AB、BA、AD、DA、EB、BE6个，所以能够进行平面镶嵌的概率P（G）=6/20=3/10．
故选B．
练习册系列答案
相关题目
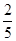现有足够多的除颜色外都相同的球供你选用，还有一个最多只能装10个球的不透明袋子.
（1）请你设计一个摸球游戏，使得从袋中任意摸出1个球，摸得红球的概率为，则应往袋中如何放球？                                                      .
（2）若袋中装有2个红球和2个白球，搅匀后从袋中摸出一个球后，不放回，然后再摸出一个球，则请用列表或画树形图的方法列出所有等可能情况，并求出两次摸出的球都是红球的概率.
一只小狗在如图所示的地板上走来走去，若黑白方砖的大小相同，则小狗最终停在黑色方砖上的概率是（   ）
A．B．C．D．
（本题满分10分）在中央电视台第2套《购物街》栏目中，有一个精彩刺激的游戏――幸运大转盘，其规则如下：
①游戏工具是一个可绕轴心自由转动的圆形转盘，转盘按圆心角均匀划分为20等分，并在其边缘标记5、10、15、…、100共20个5的整数倍数，游戏时，选手可旋转转盘，待转盘停止时，指针所指的数即为本次游戏的得分；
②每个选手在旋转一次转盘后可视得分情况选择是否再旋转转盘一次，若只旋转一次，则以该次得分为本轮游戏的得分，若旋转两次则以两次得分之和为本轮游戏的得分；
③若某选手游戏得分超过100分，则称为“爆掉”，该选手本轮游戏裁定为“输”，在得分不超过100分的情况下，分数高者裁定为“赢”；
④遇到相同得分的情况，相同得分的选手重新游戏，直到分出输赢．
现有甲、乙两位选手进行游戏，请解答以下问题：
（1）甲已旋转转盘一次，得分65分，他选择再旋转一次，求他本轮游戏不被“爆掉”的概率．
（2）若甲一轮游戏最终得分为90分，乙第一次旋转转盘得分为85分，则乙还有可能赢吗?赢的概率是多少？
（3）若甲、乙两人交替进行游戏，现各旋转一次后甲得85分，乙得65分，你认为甲是否应选择旋转第二次？说明你的理由．
从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：

根据以上数据可以估计，该玉米种子发芽的概率约为       （精确到0.1）．
三个同一天出生在同一医院的男孩，由于地震的原因，被医护人员弄混淆了，父母含辛茹苦地将“自己的孩子”养育了20年之后，却意外地发现儿子不是自己亲生……这是电视剧《今生是亲人》诱人的情节和剧中溢出的那浓浓的人间真情，剧中的三个孩子（刘震，杨抗震，高震宝）究竟各是谁家（刘，杨，高）亲生的。对于这个问题，我们可以提出一个数学问题，即：剧中的医护人员将3个孩子送给3位母亲，总共有多少种可能的结果？全送对的概率是多少？至少送对一个的概率又是多少？请你解答这个问题.
随机从三男一女四名学生的学号中抽取两个人的学号，被抽中的两人性别不同的概率为（　　）
A．B．C．D．
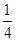
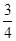
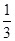
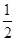
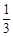在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有4个红球且摸到红球的概率为，那么口袋中球的总数为_____________．
下列事件中，必然事件是
A．度量一个三角形的三个内角，和为360B．早晨，太阳从东方升起
C．掷一次硬币，有国徽的一面向上D．买一张体育彩票中奖，中50万元

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网