题目内容
如图,直线y=-
x+4交x轴A,交y轴于B,M为OA上一点,⊙M经过B、A两点,交x轴负半轴于一点C,交y轴的负半轴于一点D.
(1)求M的坐标.
(2)BM的延长线交⊙M于E,直线BA绕B点顺时针旋转经过△OBM的内心I时交AE的延长线于K,求线段AK的长.
(3)分别过A、B两点作⊙M的切线相交于点P,过AB两点的动圆⊙N交PB的延长线于G,交y轴的负半轴于H.有两个结论:①BH+BG的值不变,②BH-BG的值不变.其中只有一个是正确的.请作出判断,并求其值.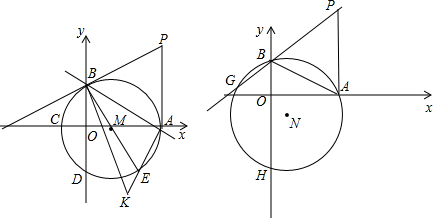
| 1 | 2 |
(1)求M的坐标.
(2)BM的延长线交⊙M于E,直线BA绕B点顺时针旋转经过△OBM的内心I时交AE的延长线于K,求线段AK的长.
(3)分别过A、B两点作⊙M的切线相交于点P,过AB两点的动圆⊙N交PB的延长线于G,交y轴的负半轴于H.有两个结论:①BH+BG的值不变,②BH-BG的值不变.其中只有一个是正确的.请作出判断,并求其值.
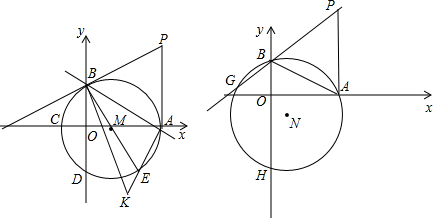
分析:(1)首先求得A、B的坐标,则M是线段AB的中垂线与x轴的交点,求得AB的垂直平分线的解析式,然后求得与x轴的交点即可;
(2)根据内心的定义以及等腰三角形的性质,和等角对等边可以证得:△BAK是等腰直角三角形,根据勾股定理求得AB,即可求得AK的长;
(3)过A作AF⊥PG于F,连接AG,AH,可以证得:△AOB≌△AFB,且Rt△FGA≌Rt△AOH,则BH-BG=(BO+OH)-BG=BO+FG-BG=BO+FB,从而证得结论.
(2)根据内心的定义以及等腰三角形的性质,和等角对等边可以证得:△BAK是等腰直角三角形,根据勾股定理求得AB,即可求得AK的长;
(3)过A作AF⊥PG于F,连接AG,AH,可以证得:△AOB≌△AFB,且Rt△FGA≌Rt△AOH,则BH-BG=(BO+OH)-BG=BO+FG-BG=BO+FB,从而证得结论.
解答:解:(1)直线y=-与x轴.y轴交点分别是A(8,0),B(0,4).
∵⊙M过A、B两点,
∴M必在AB的垂直平分线上.
∴M所在直线的斜率就是2,且过点(4,2)(该点就是AB的中点坐标)
∴M所在直线的方程就是y=2x-6
∵M在OA上,即M在x轴上
∴M(3,0)
(2)I是△OBM内心∴∠OBK=∠KBE
∵AB是⊙M的弦
∴MA=MB
∴∠MAB=∠MBA
∵∠OBK+∠KBE+∠MAB+∠MBA=90°
∴∠KBE+∠MBA=45°
∵BE是⊙M的直径
∴∠BAK=90°
∴∠K=45°
∴△BAK是等腰Rt△
∴AK=AB
AB=
=4
,
∴AK=4
;
(3)过A作AF⊥PG于F,连接AG,AH
A(8,0),B(0,4).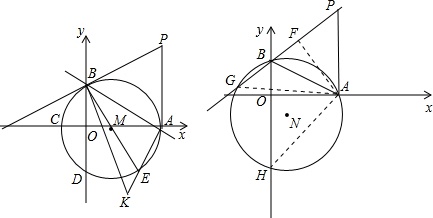
设P(8,y)
∵AP∥OB,AP=BP
∴∠PBA=∠ABO.
∴OA=OF,
在Rt△AOB和Rt△AFB中
,
∴△AOB≌△AFB(HL),
∴BO=BF
又在Rt△FGA和Rt△AOH中
∴Rt△FGA≌Rt△AOH
∴FG=HO
∴BH-BG=(BO+OH)-BG=BO+FG-BG=BO+FB=8.
∵⊙M过A、B两点,
∴M必在AB的垂直平分线上.
∴M所在直线的斜率就是2,且过点(4,2)(该点就是AB的中点坐标)
∴M所在直线的方程就是y=2x-6
∵M在OA上,即M在x轴上
∴M(3,0)
(2)I是△OBM内心∴∠OBK=∠KBE
∵AB是⊙M的弦
∴MA=MB
∴∠MAB=∠MBA
∵∠OBK+∠KBE+∠MAB+∠MBA=90°
∴∠KBE+∠MBA=45°
∵BE是⊙M的直径
∴∠BAK=90°
∴∠K=45°
∴△BAK是等腰Rt△
∴AK=AB
AB=
| 82+42 |
| 5 |
∴AK=4
| 5 |
(3)过A作AF⊥PG于F,连接AG,AH
A(8,0),B(0,4).

设P(8,y)
∵AP∥OB,AP=BP
∴∠PBA=∠ABO.
∴OA=OF,
在Rt△AOB和Rt△AFB中
|
∴△AOB≌△AFB(HL),
∴BO=BF
又在Rt△FGA和Rt△AOH中
|
∴Rt△FGA≌Rt△AOH
∴FG=HO
∴BH-BG=(BO+OH)-BG=BO+FG-BG=BO+FB=8.
点评:本题是一次函数、圆、圆的内心、以及点到直线的距离的综合应用,正确证明:△AOB≌△AFB,且Rt△FGA≌Rt△AOH是解题的关键.

练习册系列答案
相关题目
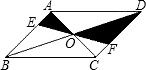 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )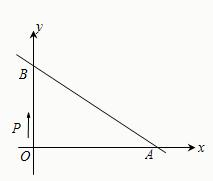 点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.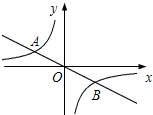 如图,直线
如图,直线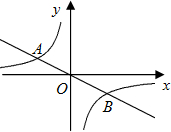 如图,直线
如图,直线