题目内容
(1998•丽水)如图,在△ABC中,AB=AC=13,BC=10,AH⊥BC,H是垂足,D是BC上的点,DE⊥AB,E是垂足,DF∥AB,交AC于点F.(1)求证:△DBE∽△ABH;
(2)设BD=x,△DEF的面积为y,写出y关于x的函数关系式;
(3)当△DEF的面积y为最大时,求tan∠EFD的值.

【答案】分析:(1)根据相似三角形的判定方法即可求;
(2)y关于x的函数关系式,根据△DEF的面积=0.5ED•DF可以得出;
(3)求tan∠EFD的值,即求ED:DF的值,由△DEF的面积y为最大,得出x的值,确定ED,DF的长度.
解答:(1)证明:∵DE⊥AB,AH⊥BC
∴∠BED=∠AHB=90°
∵∠B=∠B
∴△DBE∽△ABH.
(2)解:BC=10,BH=5,AH= =12,BD=x,CD=10-x,ED=
=12,BD=x,CD=10-x,ED=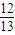 x
x
∵DF∥AB
∴DF:AB=CD:CB
∵DF=1.3(10-x)
∴y=0.5× x×1.3(10-x)=0.6x(10-x)
x×1.3(10-x)=0.6x(10-x)
(3)解:y=0.6x(10-x)=-0.6(x-5)2+15,
∵当△DEF的面积y为最大时,x=5,ED= ,DF=6.5
,DF=6.5
∴tan∠EFD=ED:DF=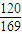
点评:本题考查相似三角形的判定和性质,三角形的面积公式,可利用数形结合思想根据题目提供的条件转化为函数关系式,同时考查了三角函数的计算.
(2)y关于x的函数关系式,根据△DEF的面积=0.5ED•DF可以得出;
(3)求tan∠EFD的值,即求ED:DF的值,由△DEF的面积y为最大,得出x的值,确定ED,DF的长度.
解答:(1)证明:∵DE⊥AB,AH⊥BC
∴∠BED=∠AHB=90°
∵∠B=∠B
∴△DBE∽△ABH.
(2)解:BC=10,BH=5,AH=
 =12,BD=x,CD=10-x,ED=
=12,BD=x,CD=10-x,ED=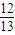 x
x∵DF∥AB
∴DF:AB=CD:CB
∵DF=1.3(10-x)
∴y=0.5×
 x×1.3(10-x)=0.6x(10-x)
x×1.3(10-x)=0.6x(10-x)(3)解:y=0.6x(10-x)=-0.6(x-5)2+15,
∵当△DEF的面积y为最大时,x=5,ED=
 ,DF=6.5
,DF=6.5∴tan∠EFD=ED:DF=
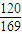
点评:本题考查相似三角形的判定和性质,三角形的面积公式,可利用数形结合思想根据题目提供的条件转化为函数关系式,同时考查了三角函数的计算.

练习册系列答案
相关题目
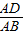 =( )
=( )

 =( )
=( )