Question

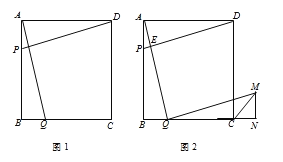
【题目】如图1，在四边形ABCD中，AB=BC=CD=AD=4cm，∠BAD=∠B=∠C=∠ADC=90°，点P以1cm/s的速度自点A向终点B运动，点Q同时以1cm/s的速度自点B向终点C运动，连接AQ、DP，设运动时间为t s．

（1）当t=　 　s时，点P到达点B；

（2）求证：在运动过程中，△ABQ≌△DAP始终成立；

（3）如图2，作QM∥PD，且QM=PD，作MN⊥射线BC于点N，连接CM，请问在Q的运动过程中，∠MCN的度数是否改变？如果不变，请求出∠MCN；如果改变，请说明理由．

Answer 1

【答案】（1）4；（2）证明见解析；（3）∠MCN=45°．

【解析】

（1）根据AB=4cm，点P以1cm/s的速度自点A向终点B运动计算即可；

（2）根据题意得到AP=BQ，利用SAS定理证明；

（3）根据全等三角形的性质得到QM=AQ，∠AQB=∠QMN，证明△AQB≌△QMN，根据全等三角形的性质得到QN=AB，MN=BQ，结合图形证明即可．

（1）∵AB=4cm，点P以1cm/s的速度自点A向终点B运动，

∴点P到达点B所用的时间为：4÷1=4（s），

故答案为：4；

（2）在运动过程中，AP=BQ=t，

在△ABQ和△DAP中，

，

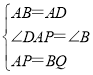∴△ABQ≌△DAP；

（3）∠MCN的度不改变，始终为45°，

理由如下：∵△ABQ≌△DAP，

∴AQ=DP，

∵QM=PD，

∴QM=AQ，

∵△ABQ≌△DAP，

∴∠BAQ=∠ADP，

∵∠BAQ+∠DAQ=90°，

∴∠ADP+∠DAQ=90°，即∠AED=90°，

∵QM∥PD，

∴∠AQM=∠AED=90°，

∴∠AQB+∠MQN=90°，

∴∠AQB=∠QMN，

在△AQB和△QMN中，

，

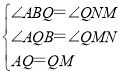∴△AQB≌△QMN，

∴QN=AB，MN=BQ，

∴BC=QN，

∴BC-QC=QN-QC，即BQ=CN，

∴MN=CN，

∴∠MCN=45°．