题目内容
如果一次函数y=kx+b中自变量x的取值范围是-1≤x≤3时，函数值y的取值范围是1≤y≤3，求这个一次函数解析式．
解：当y随x的增大而增大时，由题意得：
-k+b=1①
3k+b=3 ②1分
联立解得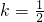
，
．2分
故这个一次函数解析式为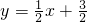
．3分
当y随x的增大而减小时，
得：-k+b=3③
3k+b=1 ④4分
联立解得：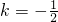
，
．5分
故这个一次函数解析式为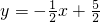
．6分
分析：自变量x的取值范围是-1≤x≤3时，函数值y的取值范围是1≤y≤3，根据条件就可以得到直线经过点（-1，1）和（3，3）或（-1，3）和（3，1），根据待定系数法就可以求出函数解析式．
点评：本题主要考查了待定系数法求函数解析式，能够想到分两种情况讨论是解决本题的关键．
-k+b=1①
3k+b=3 ②1分
联立解得
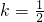，．2分故这个一次函数解析式为
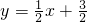．3分当y随x的增大而减小时，
得：-k+b=3③
3k+b=1 ④4分
联立解得：
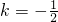，．5分故这个一次函数解析式为
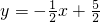．6分分析：自变量x的取值范围是-1≤x≤3时，函数值y的取值范围是1≤y≤3，根据条件就可以得到直线经过点（-1，1）和（3，3）或（-1，3）和（3，1），根据待定系数法就可以求出函数解析式．
点评：本题主要考查了待定系数法求函数解析式，能够想到分两种情况讨论是解决本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
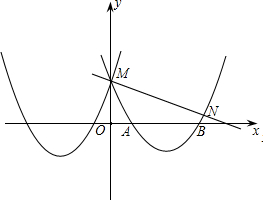点M，与x轴交于点A和B．
如果一次函数y=kx+b的图象如图所示，那么k