题目内容
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有触礁的危险?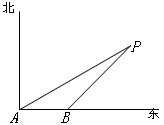

没有
试题分析:过P作PC⊥AB于C点,先求出AB的长、∠PAB、∠PBC、∠PCB的度数,即可得到PC=BC,在Rt△PAC中,根据30°角的正切函数即可求得PC的长,再与6比较即可作出判断.
过P作PC⊥AB于C点
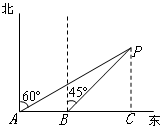
由题意得AB=18×
 =6,∠PAB=90°-60°=30°,
=6,∠PAB=90°-60°=30°,∠PBC=90°-45°=45°,∠PCB=90°,
∴PC=BC.
在Rt△PAC中,tan30°=
 ,
,即
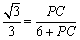 ,解得PC=
,解得PC=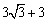 .
.∵
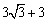 >6,
>6,∴海轮不改变方向继续前进无触礁危险.
点评:解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 .
. 
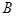 处时,得知正北方向上距
处时,得知正北方向上距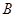 处20海里的
处20海里的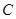 处有一渔船发生故障,就立即指挥港口
处有一渔船发生故障,就立即指挥港口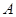 处的救援艇前往
处的救援艇前往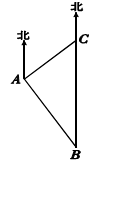
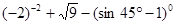 +︱1-
+︱1-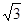 ︱.
︱.


 中,
中,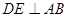 ,
,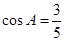 ,
,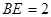 ,
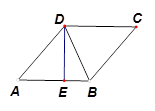
,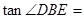 .
.
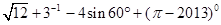 .
.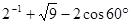
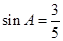 ,则菱形ABCD的面积是__________cm2.
,则菱形ABCD的面积是__________cm2.