题目内容
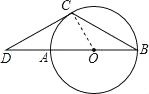
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
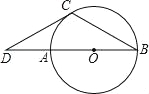
【答案】(1)证明详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据切线的判定方法,只需证CD⊥OC.所以连接OC,证∠OCD=90°;
(2)易求半径OC的长.在Rt△OCD中,运用三角函数求CD.
试题解析:(1)连接OC.
∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
∴∠COD=∠B+∠OCB=60°,
∵∠BDC=30°,
∴∠BDC+∠COD=90°,DC⊥OC,
∵BC是弦,
∴点C在⊙O上,
∴DC是⊙O的切线,点C是⊙O的切点;
(2)解:∵AB=2,
∴OC=OB=![]() =1,
=1,
∵在Rt△COD中,∠OCD=90°,∠D=30°,
∴DC=![]() OC=
OC=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目