题目内容
 (2009•河西区一模)如图,在一个正方形的工件中心挖去一个小正方形(小正方形的四边与大正方形的四边分别平方),留下一个“方环”,现在要想求这个方环的面积,但只准测量一次(即只准测一条线段的长),你能办到吗?请叙述你的方法:
(2009•河西区一模)如图,在一个正方形的工件中心挖去一个小正方形(小正方形的四边与大正方形的四边分别平方),留下一个“方环”,现在要想求这个方环的面积,但只准测量一次(即只准测一条线段的长),你能办到吗?请叙述你的方法:作正方形ABCD的外接圆,连接AO,过点E作AO的垂线交⊙O于M、N,只测量线段MN的长度就能知道这个方环的面积.
作正方形ABCD的外接圆,连接AO,过点E作AO的垂线交⊙O于M、N,只测量线段MN的长度就能知道这个方环的面积.
.分析:由图可知:方环面积=大正方形的面积-小正方形的面积,所以假设外面的大正方形是ABCD,边长是a,小正方形的边长是b,里面的小正方形与A相邻的顶点是E,那么作正方形ABCD的外接圆O,连接AO,过点E作AO的垂线交圆O于M、N,只测量线段MN的长度就能知道这个方环的面积.
解答: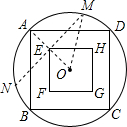 解:连接OM,AO,过点E作AO的垂线交⊙O于M、N,
解:连接OM,AO,过点E作AO的垂线交⊙O于M、N,
∵四边形ABCD是正方形,
∴OM=OA=
a,OE=
b,
∵MN⊥OA,
∴△MEO是直角三角形,ME=NF=
MN,
∴ME2=OM2-OE2=
(a2-b2),
∴(
MN)2=
(a2-b2),
即:MN2=a2-b2,
∵方环面积=a2-b2,
∴方环面积=MN2.
故答案为:作正方形ABCD的外接圆,连接AO,过点E作AO的垂线交⊙O于M、N,只测量线段MN的长度就能知道这个方环的面积.
 解:连接OM,AO,过点E作AO的垂线交⊙O于M、N,
解:连接OM,AO,过点E作AO的垂线交⊙O于M、N,∵四边形ABCD是正方形,
∴OM=OA=
| ||
| 2 |
| ||
| 2 |
∵MN⊥OA,
∴△MEO是直角三角形,ME=NF=
| 1 |
| 2 |
∴ME2=OM2-OE2=
| 1 |
| 4 |
∴(
| 1 |
| 2 |
| 1 |
| 4 |
即:MN2=a2-b2,
∵方环面积=a2-b2,
∴方环面积=MN2.
故答案为:作正方形ABCD的外接圆,连接AO,过点E作AO的垂线交⊙O于M、N,只测量线段MN的长度就能知道这个方环的面积.
点评:本题考查了正方形的性质:①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③两条对角线将正方形分成四个全等的等腰直角三角形和垂径定理以及勾股定理的运用,对训练学生的动手操作能力来说是一道不错的题目.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 (2009•河西区一模)如图所示,在半径为r的圆内作一个内接正三角形,依次再作内切圆,那么图中最小的圆的半径是( )
(2009•河西区一模)如图所示,在半径为r的圆内作一个内接正三角形,依次再作内切圆,那么图中最小的圆的半径是( ) (2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为
(2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为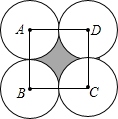 (2009•河西区一模)如图,正方形的边长为a,分别以正方形的四个顶点为圆心,以
(2009•河西区一模)如图,正方形的边长为a,分别以正方形的四个顶点为圆心,以 点P,连接AB和ED.
点P,连接AB和ED.