题目内容
【题目】如图，东湖隧道的截面由抛物线和长方形构成，长方形的长OA为12cm，宽OB为4cm，隧道顶端D到路面的距离为10cm，建立如图所示的直角坐标系 
（1）求该抛物线的解析式．
（2）一辆货运汽车载一长方体集装箱，集装箱最高处与地面距离为6m，宽为4m，隧道内设双向行车道，问这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面高度相等，如果灯离地面的高度不超过8.5m，那么两排灯的水平距离最小是多少米？
【答案】
（1）】解：根据题意，该抛物线的顶点坐标为（6，10），
设抛物线解析式为：y=a（x﹣6）2+10，
将点B（0，4）代入，得：36a+10=4，
解得：a=﹣ 
，
故该抛物线解析式为y=﹣ （x﹣6）2+10
（2）】解：根据题意，当x=6+4=10时，y=﹣ ×16+10= 
＞6，
∴这辆货车能安全通过
（3）】解：当y=8.5时，有：﹣ （x﹣6）2+10=8.5，
解得：x1=3，x2=9，
∴x2﹣x1=6，
答：两排灯的水平距离最小是6米
【解析】（1）设出抛物线的解析式，根据抛物线顶点坐标，代入解析式；（2）令x=10，求出y与6作比较；（3）求出y=8.5时x的值即可得．
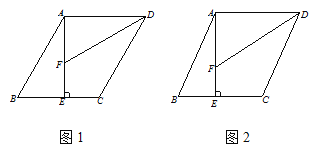
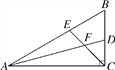
【题目】在直角△ABC中，∠ACB＝90°，∠B＝60°，AD，CE分别是∠BAC和∠BCA的平分线，AD，CE相交于点F.
(1)求∠EFD的度数；
(2)判断FE与FD之间的数量关系，并证明你的结论．
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石．某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．
(1)当x≥50时，分别求出yA，yB与x之间的函数关系式；
(2)若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？
