题目内容
一组互不相等的数据,它的中位数为80,小于中位数的数的平均数为70,大于中位数的数的平均数为96,设这组数据的平均数为
,则
=( )
. |
| x |
. |
| x |
| A、82 | ||
| B、83 | ||
C、80≤
| ||
D、82≤
|
分析:当这组数据的个数应分为奇数个与偶数个两种情况进行讨论,并且大于中位数与小于中位数的数个数相同,可以设都是m个,根据平均数的计算公式即可求解.
解答:解:大于中位数与小于中位数的数个数相同,可以设都是m个.
当这组数有偶数个时,则中位数不是这组数中的数,则这组数有2m个,则平均数是:
=83;
当这组数据的个数是奇数个时,则这组数有2m+1个,则平均数是:
=83-
,
而m≥1,因而0<
≤1
∴83-
≥83-1=82且83-
<83.
故82≤
<83.
故选D.
当这组数有偶数个时,则中位数不是这组数中的数,则这组数有2m个,则平均数是:
| 70m+96m |
| 2m |
当这组数据的个数是奇数个时,则这组数有2m+1个,则平均数是:
| 70m+96m+80 |
| 2m+1 |
| 3 |
| 2m+1 |
而m≥1,因而0<
| 3 |
| 2m+1 |
∴83-
| 3 |
| 2m+1 |
| 3 |
| 2m+1 |
故82≤
. |
| x |
故选D.
点评:本题主要考查了中位数与平均数的计算方法,注意到大于中位数与小于中位数的数个数相同,并且分两种情况进行讨论是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
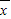 ,则
,则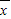 =( )
=( )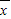 ≤82
≤82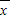 ≤83
≤83