题目内容
已知点A在直角坐标系中的坐标为(1,
),在x轴上找一点P,使得以点O,A,P为顶点的三角形是等腰三角形,则符合条件的点P有( )个.
| 3 |
分析:首先算出AO的长,再以O为圆心,AO长为半径画圆,交x轴于两点,再做出AO的垂直平分线,与x轴交点也可以构造出等腰三角形,此时为(0,2)点,得出只有两点即为P所在位置.
解答: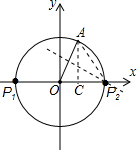 解:过点A作AC⊥x轴于点C,
解:过点A作AC⊥x轴于点C,
∵A(1,
),
∴AO=2,tan∠AOC=
=
,
∴∠AOC=60°,
以O为圆心,2为半径画圆,交x轴于两点(2,0),(-2,0),
作AO的垂直平分线,此时交点正好与(2,0)点重合,
故使得△AOP为等腰三角形,则符合条件的P点共有2个,
故选:C.
 解:过点A作AC⊥x轴于点C,
解:过点A作AC⊥x轴于点C,∵A(1,
| 3 |
∴AO=2,tan∠AOC=
| AC |
| OC |
| 3 |
∴∠AOC=60°,
以O为圆心,2为半径画圆,交x轴于两点(2,0),(-2,0),
作AO的垂直平分线,此时交点正好与(2,0)点重合,
故使得△AOP为等腰三角形,则符合条件的P点共有2个,
故选:C.
点评:此题主要考查了等腰三角形的判定,关键是掌握有两边相等的三角形是等腰三角形.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 已知点A在直角坐标系中如图:
已知点A在直角坐标系中如图: 已知点A在直角坐标系中如图:
已知点A在直角坐标系中如图: 都经过A点关于x轴的对称点A',试求m、n的值,并求直线与双曲线的另一个交点的坐标.
都经过A点关于x轴的对称点A',试求m、n的值,并求直线与双曲线的另一个交点的坐标.