题目内容
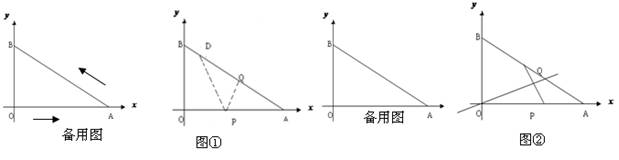
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).
(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
略
解析:解:(1)在Rt△AOB中,OA=4,OB=3
∴AB=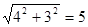
①P由O向A运动时,OP=AQ=t,AP=4-t
过Q作QH⊥AP于H点,由QH//BO得
![]()
∴![]()
即![]() (0<t≤4)
(0<t≤4)
②当4<t≤5时,AP=t-4 AQ=t
sin∠BAO=![]()
OH=![]()
∴![]()
=![]() ··············(4分)
··············(4分)
(2)由题意知,此时△APQ≌△DPQ
∠AQP=900 ∴cosA=![]()
当0<t≤4 ∴![]() 即
即![]()
当4<t≤5时,![]() t=-16(舍去)
t=-16(舍去)
∴![]() ···············(6分)
···············(6分)
(3)存在,有以下两种情况
①若PE//BQ,则等腰梯形PQBE中PQ=BE
过E、P分分别作EM⊥AB于M,PN⊥AB于N
则有BM=QN,由PE//BQ得![]()
∴![]()
又∵AP=4-t, ∴AN=![]()
∴![]() 由BM=QN,得
由BM=QN,得![]()
∴![]() ∴
∴![]() ···································(8分)
···································(8分)
②若PQ//BE,则等腰梯形PQBE中
BQ=EP且PQ⊥OA于P点
由题意知![]()
∵OP+AP=OA ∴![]()
∴![]() t··············(10分)
t··············(10分)
由①②得E点坐标为![]()
(4)①当P由O向A运动时,OQ=OP=AQ=t
可得∠QOA=∠QAO ∴∠QOB=∠QBO
∴OQ=BQ=t ∴BQ=AQ=![]() AE
AE
∴![]() ······················(11分)
······················(11分)
②当P由A向O运动时,OQ=OP=8-t
BQ=5-t, ![]()
在Rt△OGQ中,OQ2 = RG2 + OG2
即(8-t)2 =![]()
∴t = 5·························(12分)
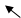

 走进文言文系列答案
走进文言文系列答案