题目内容
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
【小题1】求点B的坐标
【小题2】若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
【小题3】在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。
【小题1】(
 )
)【小题2】y=
 x2+
x2+ x.
x.【小题3】(
 ),
),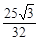 解析:
解析:(1) 在Rt△OAB中,∵∠AOB=30°,∴ OB=
 . 过点B作BD垂直于x轴,垂足为D,则 OD=
. 过点B作BD垂直于x轴,垂足为D,则 OD= ,BD=
,BD= ,∴点B的坐标为(
,∴点B的坐标为( ) .
) . (2) 将A(2,0)、B (
 )、O(0,0)三点的坐标代入y=ax2+bx+c,得
)、O(0,0)三点的坐标代入y=ax2+bx+c,得
解有a=
 ,b=
,b= ,c="0." ∴所求二次函数解析式是 y=
,c="0." ∴所求二次函数解析式是 y= x2+
x2+ x.
x.(3) 设存在点C (x ,
 x2+
x2+ x) (其中0<x<
x) (其中0<x<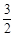 ),使四边形ABCO面积最大.
),使四边形ABCO面积最大.∵△OAB面积为定值,
∴只要△OBC面积最大,四边形ABCO面积就最大.
过点C作x轴的垂线CE,垂足为E,交OB于点F,则
S△OBC= S△OCF +S△BCF=
 =
= ,
,而 |CF|=yC-yF=
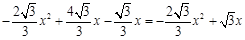 ,
,∴ S△OBC=
 .
. ∴当x=
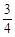 时,△OBC面积最大,最大面积为
时,△OBC面积最大,最大面积为 .
. 此时,点C坐标为(
 ),四边形ABCO的面积为
),四边形ABCO的面积为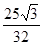 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

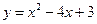 与x 轴交于两点A、B,其顶点为C.
与x 轴交于两点A、B,其顶点为C.

