题目内容
某小区有一块等腰三角形的草地,它的一边长为20m,面积为160m2,为美化小区环境,现要给这块三角形草地围上白色的低矮栅栏,则需要栅栏的长度为 m.
【答案】分析:分20m是底边和腰两种情况讨论;当是腰时又可以分为钝角三角形和锐角三角形两种情况,再次分情况讨论.
解答:解:(1)当20是等腰三角形的底边时,
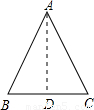
根据面积求得底边上的高AD是16,
再根据等腰三角形的三线合一,知:底边上的高也是底边上的中线,即底边的一半BD=10,
根据勾股定理即可求得其腰长AB= =
=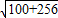 =2
=2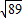 ,此时三角形的周长是20+4
,此时三角形的周长是20+4 ;
;
(2)当20是腰时,由于高可以在三角形的内部,也可在三角形的外部,又应分两种情况.
根据面积求得腰上的高是16;
①当高在三角形的外部时,
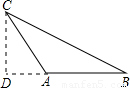
在RT△ADC中,AD= =12,从而可得BD=32,
=12,从而可得BD=32,
进一步根据勾股定理求得其底边是BC=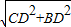 =
=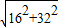 =16
=16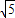 ,此时三角形的周长是40+16
,此时三角形的周长是40+16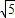 ;
;
②当高在三角形的内部时,

根据勾股定理求得AD= =12,BD=AB-AD=8,
=12,BD=AB-AD=8,
在RT△CDB中,BC=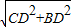 是
是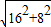 =8
=8 ,此时三角形的周长是40+8
,此时三角形的周长是40+8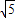 ;
;
故本题答案为:20+4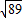 或40+16
或40+16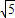 或40+8
或40+8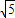 .
.
点评:此题的难点在于情况较多,注意每一种情况运用勾股定理进行计算.
解答:解:(1)当20是等腰三角形的底边时,

根据面积求得底边上的高AD是16,
再根据等腰三角形的三线合一,知:底边上的高也是底边上的中线,即底边的一半BD=10,
根据勾股定理即可求得其腰长AB=
 =
=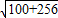 =2
=2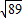 ,此时三角形的周长是20+4
,此时三角形的周长是20+4 ;
;(2)当20是腰时,由于高可以在三角形的内部,也可在三角形的外部,又应分两种情况.
根据面积求得腰上的高是16;
①当高在三角形的外部时,

在RT△ADC中,AD=
 =12,从而可得BD=32,
=12,从而可得BD=32,进一步根据勾股定理求得其底边是BC=
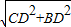 =
=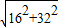 =16
=16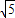 ,此时三角形的周长是40+16
,此时三角形的周长是40+16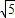 ;
;②当高在三角形的内部时,

根据勾股定理求得AD=
 =12,BD=AB-AD=8,
=12,BD=AB-AD=8,在RT△CDB中,BC=
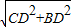 是
是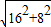 =8
=8 ,此时三角形的周长是40+8
,此时三角形的周长是40+8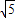 ;
;故本题答案为:20+4
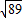 或40+16
或40+16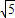 或40+8
或40+8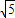 .
.点评:此题的难点在于情况较多,注意每一种情况运用勾股定理进行计算.

练习册系列答案
相关题目