题目内容
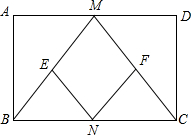 (2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=
2:1
2:1
时,四边形MENF是正方形(只写结论,不需证明)分析:(1)求出AB=DC,∠A=∠D=90°,AM=DM,根据全等三角形的判定定理推出即可;
(2)根据三角形中位线定理求出NE∥MF,NE=MF,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可;
(3)求出∠EMF=90°,根据正方形的判定推出即可.
(2)根据三角形中位线定理求出NE∥MF,NE=MF,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可;
(3)求出∠EMF=90°,根据正方形的判定推出即可.
解答:(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
∴△ABM≌△DCM(SAS);
(2)答:四边形MENF是菱形.
证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=
CM,MF=
CM,
∴NE=FM,NE∥FM,
∴四边形MENF是平行四边形,
∵△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
(3)解:当AD:AB=2:1时,四边形MENF是正方形.
理由是:∵M为AD中点,
∴AD=2AM,
∵AD:AB=2:1,
∴AM=AB,
∵∠A=90∴∠ABM=∠AMB=45°,
同理∠DMC=45°,
∴∠EMF=180°-45°-45°=90°,
∵四边形MENF是菱形,
∴菱形MENF是正方形,
故答案为:2:1.
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
|
∴△ABM≌△DCM(SAS);

(2)答:四边形MENF是菱形.
证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=
| 1 |
| 2 |
| 1 |
| 2 |
∴NE=FM,NE∥FM,
∴四边形MENF是平行四边形,
∵△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
(3)解:当AD:AB=2:1时,四边形MENF是正方形.
理由是:∵M为AD中点,
∴AD=2AM,
∵AD:AB=2:1,
∴AM=AB,
∵∠A=90∴∠ABM=∠AMB=45°,
同理∠DMC=45°,
∴∠EMF=180°-45°-45°=90°,
∵四边形MENF是菱形,
∴菱形MENF是正方形,
故答案为:2:1.
点评:本题考查了正三角形的中位线,矩形的性质,全等三角形的性质和判定,菱形、平行四边形、正方形的判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
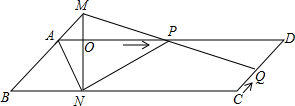 (2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
(2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1) (2013•青岛)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.
(2013•青岛)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.