题目内容
 如图,在△ABC中,O是高AD和BE的交点.
如图,在△ABC中,O是高AD和BE的交点.(1)观察图形,试猜想∠C和∠DOE、∠C和∠AOE之间具有怎样的数量关系?请说明理由;
(2)在这个解题过程中包含这样一个规律:如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为
(3)如果一个角的两边分别垂直于另一个角的两边,其中一个角比另一个角的3倍少60°,求这两个角的度数.
考点:三角形内角和定理
专题:几何图形问题
分析:(1)根据四边形的内角和定理即可得出结论;
(2)根据(1)中的结论即可得出结论;
(3)设较小的角为α,则另一个角为3α-60°,再根据(1)中的结论列出关于α的方程,求出α的值即可.
(2)根据(1)中的结论即可得出结论;
(3)设较小的角为α,则另一个角为3α-60°,再根据(1)中的结论列出关于α的方程,求出α的值即可.
解答:解:(1)∵O是高AD和BE的交点,
∴∠OEC=∠ODC=90°,
∴∠C+∠DOE=180°;
∵∠DOE+∠AOE=180°,
∴∠AOE=∠C;
(2)由(1)可知,如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为互补.
故答案为:互补;
(3)设较小的角为α,则另一个角为3α-60°,
∵α+3α-60°=180°,
解得α=60°.
∴∠OEC=∠ODC=90°,
∴∠C+∠DOE=180°;
∵∠DOE+∠AOE=180°,
∴∠AOE=∠C;
(2)由(1)可知,如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为互补.
故答案为:互补;
(3)设较小的角为α,则另一个角为3α-60°,
∵α+3α-60°=180°,
解得α=60°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
抛物线y=x2-4x-7的对称轴是( )
| A、直线x=2 |
| B、直线x=-2 |
| C、直线x=4 |
| D、直线x=7 |
某商店出售下列四种形状的地砖:
①正三角形;②正方形;③正五边形;④正六边形.
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )
①正三角形;②正方形;③正五边形;④正六边形.
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )
| A、4种 | B、3种 | C、2种 | D、1种 |
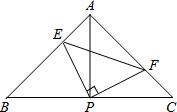 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:

 如图,直线PQ、MN被直线EF所截,交点分别为A、C,AB平分∠EAQ,CD平分∠ACN,如果PQ∥MN,那么AB与CD平行吗?为什么?
如图,直线PQ、MN被直线EF所截,交点分别为A、C,AB平分∠EAQ,CD平分∠ACN,如果PQ∥MN,那么AB与CD平行吗?为什么?