题目内容
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
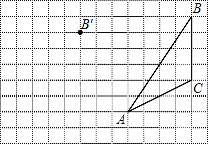
（1）在给定方格纸中画出平移后的△A′B′C′；
（2）画出AB边上的中线CD和BC边上的高线AE；
（3）线段AA′与线段BB′的关系是： ；
（4）求四边形ACBB′的面积．
【答案】（1）见解析；（2）见解析；（3）平行且相等；（4）11
【解析】
试题分析：（1）根据图形平移的性质画出△A′B′C′即可；
（2）取线段AB的中点D，连接CD，过点A作AE⊥BC的延长线与点E即可；
（3）根据图形平移的性质可直接得出结论；
（4）根据S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′即可得出结论．
解：（1）如图所示；
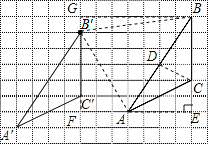
（2）如图所示；
（3）由图形平移的性质可知，AA′∥BB′，AA′=BB′．
故答案为：平行且相等；
（4）S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′
=
（7+3）×6+×4×4﹣×1×7﹣×3×5
=30﹣8﹣
﹣
=11．
练习册系列答案
相关题目
