题目内容
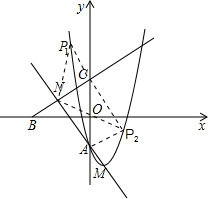
（2012•和平区模拟）如图，抛物线y=x2-2x+a（a＜0）与y轴相交于点A，顶点为M直线y=| 1 |
| 2 |
（1）填空：试用含a的代数式分别表示点M与N的坐标，则M
（1，a-1）
（1，a-1）
，N（
a，-
a）
| 4 |
| 3 |
| 1 |
| 3 |
（
a，-
a）
；| 4 |
| 3 |
| 1 |
| 3 |
（2）若点N关于y轴的对称点N′恰好落在抛物线上，求此时抛物线的解析式；
（3）在抛物线y=x2-2x+a（a＜0）上是否存在点P．使得以P、A、C、N为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由．
分析：（1）已知了抛物线的解析式，不难用公式法求出M的坐标为（1，a-1）．由于抛物线过A点，因此A的坐标是（0，a）．根据A，M的坐标，用待定系数法可得出直线AM的解析式为y=-x+a．直线AM和y=
x-a联立方程组即可求出N的坐标为（
a，-
a）．
（2）根据折叠的性质不难得出N与N′正好关于y轴对称，因此N′的坐标为（-
a，-
a）．由于N′在抛物线上，因此将N′的坐标代入抛物线的解析式中即可得出a的值．
（3）本题可分两种情况进行讨论：
①当P在y轴左侧时，如果使以P，N，A，C为顶点的四边形为平行四边形，那么P需要满足的条件是PN平行且相等于AC，也就是说，如果N点向上平移AC个单位即-2a后得到的点就是P点．然后将此时P的坐标代入抛物线中，如果没有解说明不存在这样的点P，如果能求出a的值，那么即可求出此时P的坐标．
②当P在y轴右侧时，P需要满足的条件是PN与AC应互相平分（平行四边形的对角线互相平分），那么NP必过原点，且关于原点对称．那么可得出此时P的坐标，然后代入抛物线的解析式中按①的方法求解即可．
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
（2）根据折叠的性质不难得出N与N′正好关于y轴对称，因此N′的坐标为（-
| 4 |
| 3 |
| 1 |
| 3 |
（3）本题可分两种情况进行讨论：
①当P在y轴左侧时，如果使以P，N，A，C为顶点的四边形为平行四边形，那么P需要满足的条件是PN平行且相等于AC，也就是说，如果N点向上平移AC个单位即-2a后得到的点就是P点．然后将此时P的坐标代入抛物线中，如果没有解说明不存在这样的点P，如果能求出a的值，那么即可求出此时P的坐标．
②当P在y轴右侧时，P需要满足的条件是PN与AC应互相平分（平行四边形的对角线互相平分），那么NP必过原点，且关于原点对称．那么可得出此时P的坐标，然后代入抛物线的解析式中按①的方法求解即可．
解答：解：（1）∵y=x2-2x+a=（x-1）2-1+a，
∴顶点M的坐标为；（1，a-1），
由于抛物线过A点，因此A的坐标是（0，a）．
设直线AM的解析式为y=kx+b，
则
，
解得：
，
则直线AM的解析式为：y=-x+a．
直线AM和y=
x-a联立方程组，
，
解得：
，
即可求出N的坐标为（
a，-
a）．
（2）∵由题意得点N与点N′关于y轴对称，
∴N′（-
a，-
a）．
将N′的坐标代入y=x2-2x+a得：
-
a=
a2+
a+a，
∴a1=0（不合题意，舍去），a2=-
．
∴此时抛物线的解析式为：y=x2-2x-
；
（3）存在，理由如下：
当点P在y轴的左侧时，若四边形ACPN是平行四边形，则PN平行且等于AC，
由A（0，a），C（0，-a），得AC=-2a，
则把N向上平移-2a个单位得到P，坐标为（
a，-
a），代入抛物线的解析式，
得：-
a=
a2-
a+a，
解得a1=0（不舍题意，舍去），a2=-
，
则P（-
，
）；
当点P在y轴的右侧时，若四边形APCN是平行四边形，则AC与PN互相平分，
由A（0，a），C（0，-a），则OA=OC，OP=ON．
则P与N关于原点对称，
则P（-
a，
a）；
将P点坐标代入抛物线解析式得：
a=
a2+
a+a，
解得a1=0（不合题意，舍去），a2=-
，
则P（
，-
）．
故存在这样的点P1（-
，
）或P2（
，-
），能使得以P，A，C，N为顶点的四边形是平行四边形．
故答案为：（1，a-1），（
a，-
a）．
∴顶点M的坐标为；（1，a-1），
由于抛物线过A点，因此A的坐标是（0，a）．
设直线AM的解析式为y=kx+b，
则
|
解得：
|
则直线AM的解析式为：y=-x+a．
直线AM和y=
| 1 |
| 2 |
|
解得：
|
即可求出N的坐标为（
| 4 |
| 3 |
| 1 |
| 3 |
（2）∵由题意得点N与点N′关于y轴对称，
∴N′（-
| 4 |
| 3 |
| 1 |
| 3 |
将N′的坐标代入y=x2-2x+a得：
-
| 1 |
| 3 |
| 16 |
| 9 |
| 8 |
| 3 |
∴a1=0（不合题意，舍去），a2=-
| 9 |
| 4 |
∴此时抛物线的解析式为：y=x2-2x-
| 9 |
| 4 |
（3）存在，理由如下：
当点P在y轴的左侧时，若四边形ACPN是平行四边形，则PN平行且等于AC，
由A（0，a），C（0，-a），得AC=-2a，
则把N向上平移-2a个单位得到P，坐标为（
| 4 |
| 3 |
| 7 |
| 3 |
得：-
| 7 |
| 3 |
| 16 |
| 9 |
| 8 |
| 3 |
解得a1=0（不舍题意，舍去），a2=-
| 3 |
| 8 |
则P（-
| 1 |
| 2 |
| 7 |
| 8 |
当点P在y轴的右侧时，若四边形APCN是平行四边形，则AC与PN互相平分，
由A（0，a），C（0，-a），则OA=OC，OP=ON．
则P与N关于原点对称，
则P（-
| 4 |
| 3 |
| 1 |
| 3 |
将P点坐标代入抛物线解析式得：
| 1 |
| 3 |
| 16 |
| 9 |
| 8 |
| 3 |
解得a1=0（不合题意，舍去），a2=-
| 15 |
| 8 |
则P（
| 5 |
| 2 |
| 5 |
| 8 |
故存在这样的点P1（-
| 1 |
| 2 |
| 7 |
| 8 |
| 5 |
| 2 |
| 5 |
| 8 |
故答案为：（1，a-1），（
| 4 |
| 3 |
| 1 |
| 3 |
点评：本题主要考查了待定系数法求函数解析式、平行四边形的性质等重要知识点，综合性强，能力要求较高．考查学生分类讨论，数形结合的数学思想方法．
练习册系列答案
名校课堂系列答案
相关题目
