题目内容
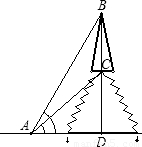
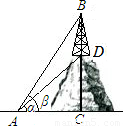
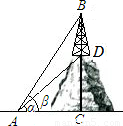
如图，从地面上点A处，测得山顶上铁塔BC的塔顶B和塔底C的仰角分别是β=60°，α=45°，已知塔高BC=100m，求小山高CD．（可用根式表示）
解：设AD=x，∵∠BAD=60°，∠CAD=45°，
则BD=AD•tan∠BAD=
AD，
CD=AD•tan∠CAD=AD，
∴BC=BD-CD=（-1）AD，
∴AD=
=（50+50）m，
∴CD=（50+50）m．
分析：根据AD和∠BAD=60°，∠CAD=45°，可以求得BD、CD的长，根据BC=BD-CD=100m，即可求得AD的值，即可解题．
点评：本题考查了特殊角的三角函数，考查了三角函数在直角三角形中的运用，本题中求BD、CD的长是解题的关键．
则BD=AD•tan∠BAD=
AD，CD=AD•tan∠CAD=AD，
∴BC=BD-CD=（
-1）AD，∴AD=
=（50+50）m，∴CD=（50
+50）m．分析：根据AD和∠BAD=60°，∠CAD=45°，可以求得BD、CD的长，根据BC=BD-CD=100m，即可求得AD的值，即可解题．
点评：本题考查了特殊角的三角函数，考查了三角函数在直角三角形中的运用，本题中求BD、CD的长是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
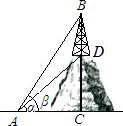如图，从地面上点A处测得山顶上铁塔BD的塔顶和塔底的仰角分别为β=60°和α=45°，已知塔高BD=100m，那么山高CD=
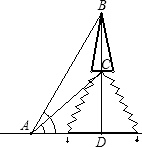如图，从地面上点A处，测得山顶上铁塔BC的塔顶B和塔底C的仰角分别是β=60°，α=45°，已知塔高BC=100m，求小山高CD．（可用根式表示）
