题目内容
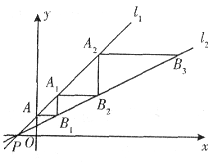
如图，直线
平行于直线
，且与直线
相交于点P（－1，0）。
（1）求直线
、
的解析式；
（2）直线与
轴交于点A，一动点C从点A出发，先沿平行于
轴的方向运动，到达直线上的点
处后，改为垂直于轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点
处后，又改为垂直于轴的方向运动，到达直线上的点
处后，仍沿平行于轴的方向运动，……，照此规律运动，动点C依次经过点，
，，，
，
，…，
，
，…。
①求点，，，的坐标；
②请你通过归纳得出点、的坐标；并求当动点C到达处时，运动的总路径的长。
解：（1）由题意，得
，解得
∴直线的解析式为
1（1分）
∵点P（－1，0）在直线上，∴
，∴
。
∴直线的解析式为
。（2分）
（2）①A点坐标为（0，1），则点的纵坐标为1。
设
∴
，∴
，∴点的坐标为（1，1）（3分）
则点的横坐标为1，设
，∴
。
∴点的坐标为（1，2）。（4分）
同理，可得
，
（6分）
②经过归纳得
，
（7分）
当动点C到达处时，运动的总路径的长为点的横纵坐标之和再减去1，
即
。（8分）
练习册系列答案
相关题目
x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．
x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．
x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．
x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．