题目内容
 如图,把一个长方形划分成二个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形长和宽之比为
如图,把一个长方形划分成二个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形长和宽之比为
- A.2:1
- B.3:1
- C.
 :1
:1 - D.
 :1
:1
C
分析:设AE=ED=a,AB=b,根据每一个小长方形与原长方形相似,可知 =
= ,再由a,b均为正数可知b=
,再由a,b均为正数可知b= a,故
a,故 =
=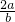 =
= =
= ,由此即可得出结论.
,由此即可得出结论.
解答: 解:设AE=ED=a,AB=b,
解:设AE=ED=a,AB=b,
∵每一个小长方形与原长方形相似,
∴ =
= ,
,
∴b2=2a2,
∵a,b均为正数,
∴b= a,
a,
∴ =
=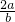 =
= =
= ,
,
∴原长方形的长与宽之比为 :1.
:1.
故选C.
点评:本题考查的相似多边形的性质,即相似多边形对应边的比叫做相似比.
分析:设AE=ED=a,AB=b,根据每一个小长方形与原长方形相似,可知
 =
= ,再由a,b均为正数可知b=
,再由a,b均为正数可知b= a,故
a,故 =
=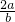 =
= =
= ,由此即可得出结论.
,由此即可得出结论.解答:
 解:设AE=ED=a,AB=b,
解:设AE=ED=a,AB=b,∵每一个小长方形与原长方形相似,
∴
 =
= ,
,∴b2=2a2,
∵a,b均为正数,
∴b=
 a,
a,∴
 =
=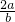 =
= =
= ,
,∴原长方形的长与宽之比为
 :1.
:1.故选C.
点评:本题考查的相似多边形的性质,即相似多边形对应边的比叫做相似比.

练习册系列答案
相关题目




 。
。
