题目内容
某校操场有一堵长方形墙面,它是由边长为a cm的24个小正方形白瓷砖拼成的.现准备在墙面上划出一块设计图案,要求面积不超过原墙面的| 1 | 3 |
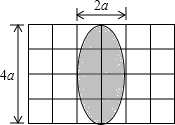
(1)小唐设计了如图的方案,图案框架的左右两边为两个半圆,中间是4个小正方形拼成的正方形.问小唐的设计方案是否符合要求请通过计算说明;

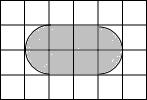
(2)你能否也设计一个符合要求的图案框架,请你把方案画在图的长方形中,并标示出尺寸(不再要求计算说明).
分析:(1)因为要求图中图案的面积不超过原墙面的
,即≤24a2÷3=8a2,那么作图时应该以不超过8个正方形的面积为准;
(2)按要求作图,作图时应该以不超过8个正方形的面积即可.
| 1 |
| 3 |
(2)按要求作图,作图时应该以不超过8个正方形的面积即可.
解答:解:(1)S长方形=24a2cm2,
S框架=4a2+πa2=(4+π)a2cm2,(2分)
∵(4+π)a2<(4+4)a2=8a2,
∴S框架<
S长方形,(4)
∴设计符合要求;(5分)
(2)
学生作出图形给(1分),设计符合要求给(2分).
S框架=4a2+πa2=(4+π)a2cm2,(2分)
∵(4+π)a2<(4+4)a2=8a2,
∴S框架<
| 1 |
| 3 |
∴设计符合要求;(5分)
(2)

学生作出图形给(1分),设计符合要求给(2分).
点评:此题主要考查学生的创作能力和审美能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.

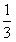 。
。
