题目内容
 已知,∠CGD=∠CAB,∠1=∠2,EF⊥BC,试说明:AD⊥BC.
已知,∠CGD=∠CAB,∠1=∠2,EF⊥BC,试说明:AD⊥BC.
证明:∵∠CGD=∠CAB,
∴DG∥AB(同位角相等,两直线平行);
∴∠1=∠3(两直线平行,内错角相等);
又∵∠1=∠2,
∴∠2=∠3(等量代换),
∴EF∥AD(同位角相等,两直线平行);
而EF⊥BC,
∴AD⊥BC.
分析:由同位角∠CGD=∠CAB推知两直线DG∥AB,所以内错角∠1=∠3;然后由已知条件和等量代换求得同位角∠2=∠3;所以两直线EF∥AD;最后根据平行线中的一条垂直于另一条直线,则另一条平行线也垂直于同一条直线证得AD⊥BC.
点评:本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.
∴DG∥AB(同位角相等,两直线平行);
∴∠1=∠3(两直线平行,内错角相等);
又∵∠1=∠2,
∴∠2=∠3(等量代换),
∴EF∥AD(同位角相等,两直线平行);
而EF⊥BC,
∴AD⊥BC.
分析:由同位角∠CGD=∠CAB推知两直线DG∥AB,所以内错角∠1=∠3;然后由已知条件和等量代换求得同位角∠2=∠3;所以两直线EF∥AD;最后根据平行线中的一条垂直于另一条直线,则另一条平行线也垂直于同一条直线证得AD⊥BC.
点评:本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
 20、已知,∠CGD=∠CAB,∠1=∠2,EF⊥BC,试说明:AD⊥BC.
20、已知,∠CGD=∠CAB,∠1=∠2,EF⊥BC,试说明:AD⊥BC. 21、如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
21、如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: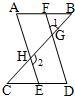 14、根据下列推理过程填空,并在括号内加注理由.
14、根据下列推理过程填空,并在括号内加注理由.