题目内容
设函数y=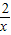 与y=x-1的图象的交点坐标为(a,b),则
与y=x-1的图象的交点坐标为(a,b),则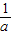 -
-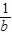 的值为 .
的值为 .
【答案】分析:把交点坐标代入2个函数后,得到2个方程,求得a,b的解,整理求得 -
-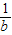 的值即可.
的值即可.
解答:解:∵函数y=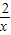 与y=x-1的图象的交点坐标为(a,b),
与y=x-1的图象的交点坐标为(a,b),
∴b=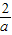 ,b=a-1,
,b=a-1,
∴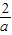 =a-1,
=a-1,
a2-a-2=0,
(a-2)(a+1)=0,
解得a=2或a=-1,
∴b=1或b=-2,
∴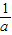 -
- 的值为-
的值为- .
.
故答案为:- .
.
点评:考查函数的交点问题;得到2个方程判断出a,b的值是解决本题的关键.
 -
-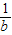 的值即可.
的值即可.解答:解:∵函数y=
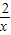 与y=x-1的图象的交点坐标为(a,b),
与y=x-1的图象的交点坐标为(a,b),∴b=
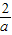 ,b=a-1,
,b=a-1,∴
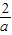 =a-1,
=a-1,a2-a-2=0,
(a-2)(a+1)=0,
解得a=2或a=-1,
∴b=1或b=-2,
∴
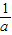 -
- 的值为-
的值为- .
.故答案为:-
 .
.点评:考查函数的交点问题;得到2个方程判断出a,b的值是解决本题的关键.

练习册系列答案
相关题目
 与y=x﹣1的图象的交点坐标为(a,b),则
与y=x﹣1的图象的交点坐标为(a,b),则 ﹣
﹣ 的值为 __________________
的值为 __________________ 与y=x﹣1的图象的交点坐标为(a,b),则
与y=x﹣1的图象的交点坐标为(a,b),则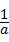 ﹣
﹣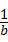 的值为 __________________
的值为 __________________ 与y=x﹣1的图象的交点坐标为(a,b),则
与y=x﹣1的图象的交点坐标为(a,b),则 ﹣
﹣ 的值为 __________________
的值为 __________________ 与y=x-1的图象的交点坐标为(a,b),则
与y=x-1的图象的交点坐标为(a,b),则 -
- 的值为 .
的值为 .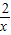 与y=x-1的图象的交点坐标为(a,b),则
与y=x-1的图象的交点坐标为(a,b),则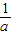 -
-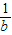 的值为 .
的值为 .