题目内容
【题目】如图,△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,B,C,D在同一直线上,连接EC.求证:EC⊥BD. 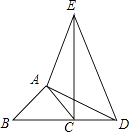
【答案】证明:∵在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC+∠CAD=∠EAD+∠CAD,∠ABC=∠BCA=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE 中,
∴△ABD≌△ACE,
∴∠ACE=∠ABD=∠ABC=45°,
∴∠BCA+∠ACE=90°,
∴EC⊥BD
【解析】先根据∠BAC+∠CAD=∠EAD+∠CAD,得出∠BAD=∠CAE,然后证明△ABD≌△ACE,再得出∠ACE=∠ABD=45°,∠BCA+∠ACE=90°,即可证明出EC⊥BD.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目

