Question

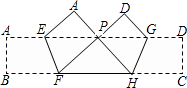
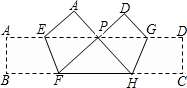
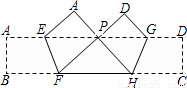
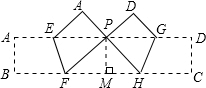
如图，把矩形纸条ABCD沿EF，GH同时折叠，B，C两点恰好落在AD边的P点处，若∠FPH=90°，PF=8，PH=6，则矩形ABCD的面积为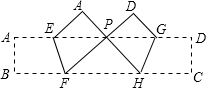

 

．

Answer 1

分析：首先根据勾股定理求得FH的长，根据折叠的性质，得BC=PF+PH+FH，再根据直角三角形的面积公式求得直角三角形FPH斜边上的高，即为AB的长，进一步求得矩形ABCD的面积．

解答：解：作PM⊥BC于M．

∵∠FPH=90°，PF=8，PH=6，
∴FH=10，AB=PM=

PF•PH

FH

=4.8．
∴BC=PF+PH+FH=24，
∴矩形ABCD的面积=AB•BC=115.2．

点评：此题综合运用了折叠的性质、勾股定理以及直角三角形的面积公式．