已知C为直线AB上的点.AB=5.BC=6.则AC=11或111或1．题目和参考答案——青夏教育精英家教网—

题目内容

已知C为直线AB上的点，AB=5，BC=6，则AC=

11或1

．

分析：分类讨论：当C点在射线AB上，则AC=AB+BC；当C点在射线BA上，则AC=CB-AB，然后把AB=5，BC=6分别代入计算即可．

解答：解：当C点在射线AB上，如图1，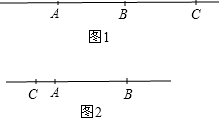

则AC=AB+BC，
而AB=5，BC=6，
∴AC=5+6=11；
当C点在射线BA上，如图2，
则AC=CB-AB，
∴AC=6-5=1，
∴AC的长为11或1．
故答案为11或1．

点评：本题考查了两点间的距离：两点之间的连线段的长叫这两点之间的距离．也考查了分类讨论思想的运用．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

．
（2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF的数量关系是否仍然成立？如成立请写出关系式；如不成立请说明理由．
（3）在图3中，若∠COF=65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．

33、已知O为直线AB上的一点，∠COE是直角，OF 平分∠AOE．
（1）如图1，若∠COF=34°，则∠BOE=

．
（2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF的数量关系是否仍然成立？请说明理由．

已知O为直线AB上的一点，∠COE是直角， OF 平分∠AOE．

（1）如图①，若∠COF＝34°，则∠BOE＝ °；若∠COF＝m°，则∠BOE＝ °；由上面的解答可知：∠BOE与∠COF之间的数量关系应该为．
（2）如图②，（1）中∠BOE与∠COF之间的数量关系是否仍然成立？若成立，请给予证明；若不成立，请说明理由．
（3）如图③，在（2）的情况下，若∠COF＝65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．

已知O为直线AB上的一点，∠COE是直角， OF 平分∠AOE．

（1）如图①，若∠COF＝34°，则∠BOE＝ °；若∠COF＝m°，则∠BOE＝ °；由上面的解答可知：∠BOE与∠COF之间的数量关系应该为．

（2）如图②，（1）中∠BOE与∠COF之间的数量关系是否仍然成立？若成立，请给予证明；若不成立，请说明理由．

（3）如图③，在（2）的情况下，若∠COF＝65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．

试题分类