题目内容
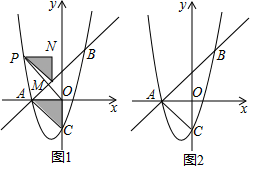
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx﹣3与直线y=x+3交于点A(m,0)和点B(2,n),与y轴交于点C.
(1)求m,n的值及抛物线的解析式;
(2)在图1中,把△AOC平移,始终保持点A的对应点P在抛物线上,点C,O的对应点分别为M,N,连接OP,若点M恰好在直线y=x+3上,求线段OP的长度;
(3)如图2,在抛物线上是否存在点Q(不与点C重合),使△QAB和△ABC的面积相等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3,m=﹣3,n=5;(2)3![]() 或
或![]() ;(3)存在;Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5),理由见解析
;(3)存在;Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5),理由见解析
【解析】
(1)把点A(m,0)和点B(2,n)代入直线y=x+3,解得:m=﹣3,n=5,A(﹣3,0)、B(2,5),把A、B坐标代入抛物线解析式即可求解;
(2)由平移得:PN=OA=3,NM=OC=3,设:平移后点P(t,t2+2t﹣3),则N(t+3,t2+2t﹣3),M(t+3,t2+2t﹣6),根据点M在直线y=x+3上,即可求解;
(3)存在.设:直线AB交y轴于D(0,3),点C关于点D的对称点为C′(0,9)按照△QAB和△Q′AB和△ABC的面积相同即可求解.
解:(1)把点A(m,0)和点B(2,n)代入直线y=x+3,解得:m=﹣3,n=5,
∴A(﹣3,0)、B(2,5),把A、B坐标代入抛物线解析式,解得:a=1,b=2,
∴抛物线解析式为:y=x2+2x﹣3…①,
则C(0,﹣3);
(2)由平移得:PN=OA=3,NM=OC=3,
设:平移后点P(t,t2+2t﹣3),则N(t+3,t2+2t﹣3),
∴M(t+3,t2+2t﹣6),∵点M在直线y=x+3上,
∴t2+2t﹣6=t+3+3,解得:t=3或﹣4,
∴P点坐标为(3,12)或(﹣4,5),
则线段OP的长度为:3![]() 或
或![]() ;
;
(3)存在.
设:直线AB交y轴于D(0,3),点C关于点D的对称点为C′(0,9)
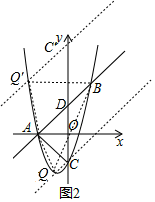
过点C和C′分别做AB的平行线,交抛物线于点Q、Q′,
则:△QAB和△Q′AB和△ABC的面积相同,
直线QC和Q′C的方程分别为:y=x﹣3和y=x+9…②,
将①、②联立,解得:x=﹣1或x=3或x=﹣4,
∴Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5).

【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
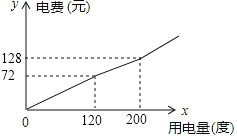
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?