题目内容
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
(1)直接写出点A,C,P的坐标.
(2)画出这个函数的图象.
【答案】(1)A(-1,0),C(0,-3),P(1,-4);(2)画图见解析.
【解析】
(1)把二次函数的一般形式变形为交点式和顶点式,即可得出点A、点B坐标和顶点P的坐标,当x=0时,y=-3,可得C点坐标;
(2)根据点C坐标和对称轴可得点C关于对称轴对称的点的坐标,利用描点法画出二次函数图象即可.
(1)∵y=x2-2x-3=(x+1)(x-3)=(x-1)2-4,
∴图象与x轴交点为(-1,0)和(3,0),顶点P坐标为(1,-4),
∵点A在点B左侧,
∴A(-1,0),
∵当x=0时,y=-3,
∴点C坐标为(0,-3).
(2)∵C(0,-3),对称轴为x=1,
∴点C关于直线x=1的对称点为(2,-3),
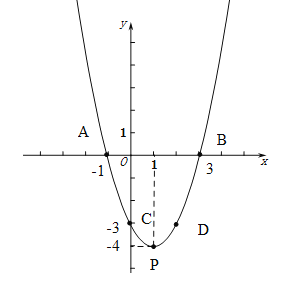
∴二次函数图象如图所示:

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④