题目内容
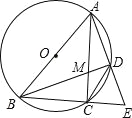
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
(1)求证:BCCE=ACMC;
(2)若点D是劣弧AC的中点,tan∠ACD=![]() ,MDBD=10,求⊙O的半径.
,MDBD=10,求⊙O的半径.
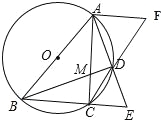
(3)若CD∥AB,过点A作AF∥BC,交CD的延长线于点F,求![]() ﹣
﹣![]() 的值.
的值.
【答案】(1)见试题解析;(2)5;(3)1.
【解析】
试题分析:(1)要证明BCCE=ACMC,即证明![]() =
=![]() ,即证明△CBM∽△CAE;
,即证明△CBM∽△CAE;
(2)因为点D是劣弧![]() 的中点,所以
的中点,所以![]() =
=![]() ,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=
,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=![]() ,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
(3)因为CD∥AB,AF∥BC,所以△CDE∽△BAE,△ADF∽△DEC,利用对边的比相等可得![]() =
=![]() ,所以
,所以![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() .
.
试题解析:(1)∵![]() =
=![]() ,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴
,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴![]() =
=![]() ,∴BCCE=ACMC;
,∴BCCE=ACMC;
(2)∵点D是劣弧![]() 的中点,∴
的中点,∴![]() =
=![]() ;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
∴∠ABD=∠CAE=∠ACD,∵AB是⊙O的直径,∴∠ADB=90°,∴△AMD∽△BAD,
∴![]() =
=![]() ,∴AD2=MDBD=10,∴AD=
,∴AD2=MDBD=10,∴AD=![]() ,∵tan∠ACD=tan∠ABD=
,∵tan∠ACD=tan∠ABD=![]() ,∴
,∴![]() ,
,
∴BD=3![]() ,∵AB2=AD2+BD2,∴AB=
,∵AB2=AD2+BD2,∴AB=![]() =10,∴⊙O的半径为:
=10,∴⊙O的半径为:![]() AB=5;
AB=5;
(3)∵CD∥AB,∴△CDE∽△BAE,∴![]() =
=![]() ,∵AF∥CE,∴△ADF∽△DEC,
,∵AF∥CE,∴△ADF∽△DEC,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =1.
=1.

 名校课堂系列答案
名校课堂系列答案【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是______元;②月销量是______件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?