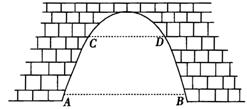
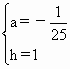题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
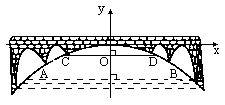
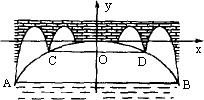
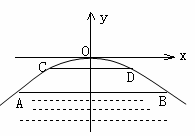
解:设抛物线的解析式为y=ax2,桥拱最高点O到水面CD的距离h cm,则有:D(5,-h)B(10,-h-3) ∴ ∴抛物线的解析式为y=- |
(2) |
水位由CD涨到点O的时间为: 1÷0.25=4h 货车按原来速度行驶不能安全通过此桥. 设货车速度提高到x km/h. 当4x+40×1=280h时x=60. ∴要使货车安全通过此桥,货车的速度应超过60km/h. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目