题目内容
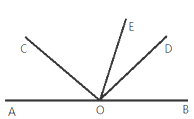
【题目】如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
【答案】(1)∠DOE=21 ;(2)∠AOC=40 .
【解析】试题分析:(1)由∠AOC=46°可求出∠BOC=134,由OE是∠BOC的平分线可求出∠BOE=67,然后根据∠DOE=∠BOE-∠BOD可求出∠DOE的度数;(2)设∠AOC的度数为x,则∠BOE=x+30 ,根据∠AOC+∠BOC=180°列方程求解.
解:(1)∵∠AOC=46°
∴∠BOC=180--∠AOC =180 -46 =134
又∵OE是∠BOC的平分线
∴∠BOE=![]() ∠BOC=67
∠BOC=67
又∵∠BOD=∠AOC= =46
∴∠DOE=∠BOE-∠BOD=67--46=21
(2)设∠AOC的度数为x,则∠BOD=x,则∠BOE=x+30
∵OE是∠BOC的平分线
∴∠BOC=2∠BOE=2(x+30 )
则有:x+2(x+30 )=180
解得:x=40
∴∠AOC=40

练习册系列答案
相关题目