题目内容
 如图,P是双曲线y=
如图,P是双曲线y=| 4 | x |
(1)求当x为何值时,⊙P与直线y=3相切,并求点P的坐标.
(2)直接写出当x为何值时,⊙P与直线y=3相交、相离.
分析:(1)利用切线的性质以及反比例函数的性质即可得出,P点的坐标应该有两个求出即可;
(2)利用函数图象进而得出符合要求的答案.
(2)利用函数图象进而得出符合要求的答案.
解答: 解:(1)设点P的坐标为(x,y),
解:(1)设点P的坐标为(x,y),
∵P是双曲线y=
(x>0)的一个分支上的一点,
∴xy=k=4,
∵⊙P与直线y=3相切,
∴p点纵坐标为:2,
∴p点横坐标为:2,
∵⊙P′与直线y=3相切,
∴p点纵坐标为:4,
∴p点横坐标为:1,
∴x=1或2,
P的坐标(1,4)或(2,2);
(2)结合图象,即可得出:
当1<x<2时,⊙P与直线y=3相交,
当x>2或0<x<1时,⊙P与直线y=3相离.
 解:(1)设点P的坐标为(x,y),
解:(1)设点P的坐标为(x,y),∵P是双曲线y=
| 4 |
| x |
∴xy=k=4,
∵⊙P与直线y=3相切,
∴p点纵坐标为:2,
∴p点横坐标为:2,
∵⊙P′与直线y=3相切,
∴p点纵坐标为:4,
∴p点横坐标为:1,
∴x=1或2,
P的坐标(1,4)或(2,2);
(2)结合图象,即可得出:
当1<x<2时,⊙P与直线y=3相交,
当x>2或0<x<1时,⊙P与直线y=3相离.
点评:此题主要考查了反比例函数的性质以及切线的性质和直线与圆的位置关系,利用数形结合解决问题是解题关键.

练习册系列答案
相关题目
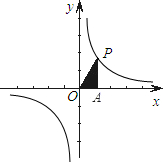 如图,P是双曲线y=
如图,P是双曲线y=| k |
| x |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、-2 |
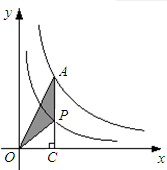 如图,P是双曲线y=
如图,P是双曲线y= (2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为
(2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为 如图,A是双曲线
如图,A是双曲线