题目内容
（2006•昆明）如图，某建筑物BC的楼顶上有一避雷针AB，在距此建筑物12米的D处安置一高度为1.5米的测倾器DE，测得避雷针顶端的仰角为60°．又知建筑物共有六层，每层层高为3米．求避雷针AB的长度．（结果精确到0.1米）（参考数据：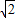
≈1.41，
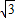≈1.73）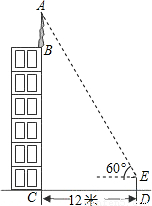
【答案】分析：首先分析图形：根据题意构造直角三角形△AEF；解其可得AF的长，再求出AC的长度，进而借助AC=AF+FC可解即可求出答案．
解答：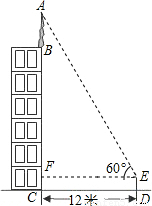
解：过点E作EF⊥AC交AC于点F，则∠AFE=90°，
四边形FCDE是矩形，EF=CD=12，
在Rt△AFE中，tan∠AEF=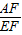
，
∴AF=12tan60°=12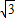
．
而FC=ED=1.5，
∴AC=AF+FC=12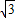
+1.5，BC=3×6=18，
∴AB=AC-BC=12
-16.5≈4.3（米）．
答：避雷针AB的长度约为4.3米．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
解答：
解：过点E作EF⊥AC交AC于点F，则∠AFE=90°，四边形FCDE是矩形，EF=CD=12，
在Rt△AFE中，tan∠AEF=
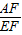，∴AF=12tan60°=12
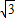．而FC=ED=1.5，
∴AC=AF+FC=12
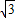+1.5，BC=3×6=18，∴AB=AC-BC=12
-16.5≈4.3（米）．答：避雷针AB的长度约为4.3米．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
