题目内容
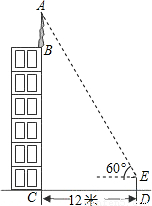
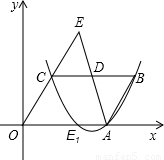
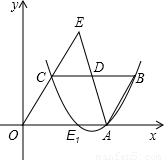
(2006•昆明)如图,在直角坐标系中,O为坐标原点,平行四边形OABC的边OA在x轴上,∠B=60°,OA=6,OC=4,D是BC的中点,延长AD交OC的延长线于点E.(1)画出△ECD关于边CD所在直线为对称轴的对称图形△E1CD,并求出点E1的坐标;
(2)求经过C、E1、B三点的抛物线的函数表达式;
(3)请探求经过C、E1、B三点的抛物线上是否存在点P,使以点P、B、C为顶点的三角形与△ECD相似?若存在这样的点P,请求出点P的坐标;若不存在这样的点P,请说明理由.
【答案】分析:(1)欲画△ECD关于边CD所在直线为对称轴的对称图形△E1CD,由CD不变,知关键是确定E1点,可过点E作对称轴CD的垂线,垂足为F,延长EF到E1,使E1F=EF.则点E1就是点E关于CD所在直线的对称点;
(2)由(1)求得E1坐标,再求抛物线的函数表达式,可通过待定系数法,利用已知条件求解;
(3)问题较难,根据两个三角形相似的条件,需要分情况讨论P在不同位置时的情况.
解答:解:(1)过点E作EE1⊥CD交BC于F点,交x轴于E1点,
则E1点为E的对称点.连接DE1、CE1,则△CE1D为所画的三角形,
∵△CED∽△OEA,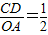 ,∴
,∴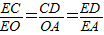 ,
,
∵EF、EE1分别是△CED、△OEA的对应高,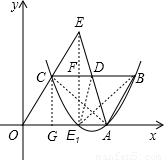
∴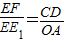 =
= ,
,
∴EF= EE1,
EE1,
∴F是EE1的中点,
∴E点关于CD的对称点是E1点,△CE1D为△CED关于CD的对称图形,
在Rt△EOE1,OE1=cos60°×EO= ×8=4,
×8=4,
∴E1点的坐标为(4,0);
(2)∵平行四边形OABC的高为h=sin60°×4=2 ,
,
过C作CG⊥OA于G,则OG=2,
∴C、B点的坐标分别为(2,2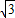 ),(8,2
),(8,2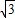 ),
),
∵抛物线过C、B两点,且CB∥x轴,C、B两点关于抛物线的对称轴对称,
∴抛物线的对称轴方程为x=5,
又∵抛物线经过E1(4,0),
则抛物线与x轴的另一个交点为A(6,0),
∴可设抛物线为y=a(x-4)(x-6),
∵点C(2,2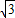 )在抛物线上,
)在抛物线上,
∴2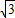 =a(2-4)(2-6),
=a(2-4)(2-6),
解得a=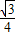 ,
,
∴y=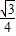 (x-4)(x-6)=
(x-4)(x-6)=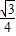 x2-
x2-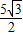 x+6
x+6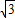 ;
;
(3)根据两个三角形相似的条件,由于在△ECD中,∠ECD=60°,
若△BCP与△ECD相似,则△BCP中必有一个角为60°,
下面进行分类讨论:
①当P点直线CB的上方时,由于△PCB中,∠CBP>90°或∠BCP>90°,
∴△PCB为钝角三角形,
又∵△ECD为锐角三角形,
∴△ECD与△CPB不相似.
从而知在直线CB上方的抛物线上不存在点P使△CPB与△ECD相似;
②当P点在直线CB上时,点P与C点或B点重合,不能构成三角形,
∴在直线CB上不存在满足条件的P点;
③当P点在直线CB的下方时,若∠BCP=60°,则P点与E1点重合,
此时,∠ECD=∠BCE1,而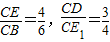 ,
,
∴ ,
,
∴△BCE与△ECD不相似,
若∠CBP=60°,则P点与A点重合,
根据抛物线的对称性,同理可证△BCA与△CED不相似,
若∠CPB=60°,假设抛物线上存在点P使△CPB与△ECD相似,
∴EF=sin60°×4=2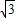 ,FD=1,
,FD=1,
∴ED=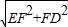 =
=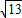 ,
,
设△ECD的边DE上的高为h1,则有 h1×ED=
h1×ED= EF×CD,
EF×CD,
∴h1=EF×CD÷ED=2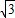 ×3÷
×3÷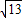 =6
=6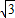 ÷
÷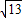 =
=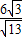 ,
,
设△CPB的边BC上的高为h2,△CPB与△ECD相似,
∵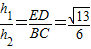 ,
,
解得h2=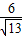 ×h1=
×h1=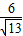 ×
×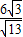 =
=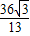 ,
,
∵抛物线的顶点坐标为(5,-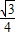 ),
),
∴抛物线的顶点到直线BC的距离d=|-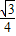 |+2
|+2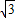 =
=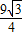 ,
,
∵h2>d,
∴所求P点到直线BC的距离大于抛物线的顶点到直线BC的距离,
从而使△CPB与△ECD相似的点P不会在抛物线上,
∴在直线CB下方不存在抛物线上的点P使△CPB与△ECD相似.
综上所述,抛物线上不存在点P使点P、B、C为顶点的三角形与△ECD相似.
点评:(1)考查的是作简单平面图形轴对称后的图形,其依据是轴对称的性质.
基本作法:①先确定图形的关键点;
②利用轴对称性质作出关键点的对称点;
③按原图形中的方式顺次连接对称点.
(2)用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法.
(3)是一道难度较大的二次函数题,综合考查了三角形相似的性质,需注意分类讨论,全面考虑点P所在位置的各种情况.
(2)由(1)求得E1坐标,再求抛物线的函数表达式,可通过待定系数法,利用已知条件求解;
(3)问题较难,根据两个三角形相似的条件,需要分情况讨论P在不同位置时的情况.
解答:解:(1)过点E作EE1⊥CD交BC于F点,交x轴于E1点,
则E1点为E的对称点.连接DE1、CE1,则△CE1D为所画的三角形,
∵△CED∽△OEA,
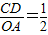 ,∴
,∴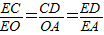 ,
,∵EF、EE1分别是△CED、△OEA的对应高,

∴
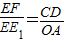 =
= ,
,∴EF=
 EE1,
EE1,∴F是EE1的中点,
∴E点关于CD的对称点是E1点,△CE1D为△CED关于CD的对称图形,
在Rt△EOE1,OE1=cos60°×EO=
 ×8=4,
×8=4,∴E1点的坐标为(4,0);
(2)∵平行四边形OABC的高为h=sin60°×4=2
 ,
,过C作CG⊥OA于G,则OG=2,
∴C、B点的坐标分别为(2,2
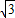 ),(8,2
),(8,2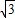 ),
),∵抛物线过C、B两点,且CB∥x轴,C、B两点关于抛物线的对称轴对称,
∴抛物线的对称轴方程为x=5,
又∵抛物线经过E1(4,0),
则抛物线与x轴的另一个交点为A(6,0),
∴可设抛物线为y=a(x-4)(x-6),
∵点C(2,2
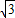 )在抛物线上,
)在抛物线上,∴2
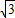 =a(2-4)(2-6),
=a(2-4)(2-6),解得a=
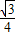 ,
,∴y=
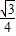 (x-4)(x-6)=
(x-4)(x-6)=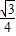 x2-
x2-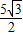 x+6
x+6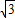 ;
;(3)根据两个三角形相似的条件,由于在△ECD中,∠ECD=60°,
若△BCP与△ECD相似,则△BCP中必有一个角为60°,
下面进行分类讨论:
①当P点直线CB的上方时,由于△PCB中,∠CBP>90°或∠BCP>90°,
∴△PCB为钝角三角形,
又∵△ECD为锐角三角形,
∴△ECD与△CPB不相似.
从而知在直线CB上方的抛物线上不存在点P使△CPB与△ECD相似;
②当P点在直线CB上时,点P与C点或B点重合,不能构成三角形,
∴在直线CB上不存在满足条件的P点;
③当P点在直线CB的下方时,若∠BCP=60°,则P点与E1点重合,
此时,∠ECD=∠BCE1,而
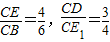 ,
,∴
 ,
,∴△BCE与△ECD不相似,
若∠CBP=60°,则P点与A点重合,
根据抛物线的对称性,同理可证△BCA与△CED不相似,
若∠CPB=60°,假设抛物线上存在点P使△CPB与△ECD相似,
∴EF=sin60°×4=2
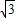 ,FD=1,
,FD=1,∴ED=
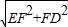 =
=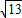 ,
,设△ECD的边DE上的高为h1,则有
 h1×ED=
h1×ED= EF×CD,
EF×CD,∴h1=EF×CD÷ED=2
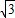 ×3÷
×3÷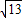 =6
=6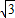 ÷
÷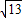 =
=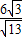 ,
,设△CPB的边BC上的高为h2,△CPB与△ECD相似,
∵
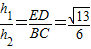 ,
,解得h2=
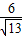 ×h1=
×h1=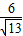 ×
×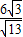 =
=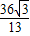 ,
,∵抛物线的顶点坐标为(5,-
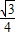 ),
),∴抛物线的顶点到直线BC的距离d=|-
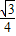 |+2
|+2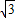 =
=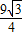 ,
,∵h2>d,
∴所求P点到直线BC的距离大于抛物线的顶点到直线BC的距离,
从而使△CPB与△ECD相似的点P不会在抛物线上,
∴在直线CB下方不存在抛物线上的点P使△CPB与△ECD相似.
综上所述,抛物线上不存在点P使点P、B、C为顶点的三角形与△ECD相似.
点评:(1)考查的是作简单平面图形轴对称后的图形,其依据是轴对称的性质.
基本作法:①先确定图形的关键点;
②利用轴对称性质作出关键点的对称点;
③按原图形中的方式顺次连接对称点.
(2)用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法.
(3)是一道难度较大的二次函数题,综合考查了三角形相似的性质,需注意分类讨论,全面考虑点P所在位置的各种情况.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

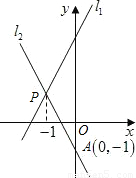
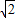 ≈1.41,
≈1.41,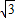 ≈1.73)
≈1.73)