题目内容
【题目】如图,已知ABCD的周长为8 cm,∠B=30°,若边长AB为x cm.
(1)写出ABCD的面积y(cm2)与x(cm)的函数关系式,并求自变量x的取值范围.

(2)当x取什么值时,y的值最大?并求出最大值.
【答案】(1)、y=-![]() +2x(0<x<4);(2)、x=2时,y的最大值为2.
+2x(0<x<4);(2)、x=2时,y的最大值为2.
【解析】
试题分析:(1)、过A作AE⊥BC,从而得出AE=![]() x,根据周长得出BC=4-x,根据平行四边形的面积得出函数解析式;(2)、将其化成顶点式,然后得出最大值.
x,根据周长得出BC=4-x,根据平行四边形的面积得出函数解析式;(2)、将其化成顶点式,然后得出最大值.
试题解析:(1)、过A作AE⊥BC于E,∵∠B=30°,AB=x, ∴AE=![]() x,又∵平行四边形ABCD的周长为8 cm,
x,又∵平行四边形ABCD的周长为8 cm,
∴BC=4-x,∴y=AE·BC=![]() x(4-x), 即y=-
x(4-x), 即y=-![]()
![]() +2x(0<x<4).
+2x(0<x<4).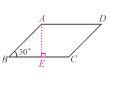
(2)、y=-![]()
![]() +2x=-
+2x=-![]()
![]() +2, ∵a=-
+2, ∵a=-![]() ,∴当x=2时,y有最大值,其最大值为2.
,∴当x=2时,y有最大值,其最大值为2.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目