题目内容
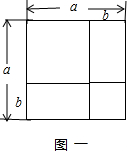
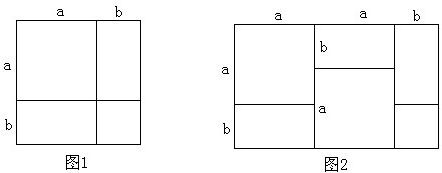
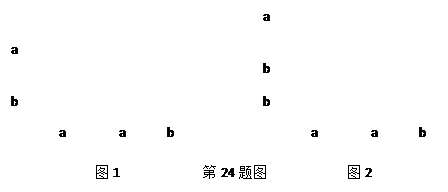
26、我们已经知道，利用图形面积可以解释代数恒等式的正确性．如完全平方公式可以用图1的面积表示．
（1）根据图2写出一个代数恒等式
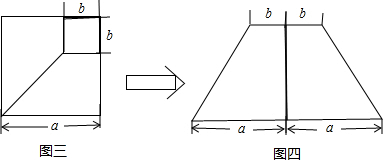
（2）其实图形的面积也可以解释不等式的正确性．如已知正数a、b、c和m、n、l，并且满足a+m=b+n=c+l=k．试构造边长为k的正方形，利用其来说明al+bm+cn＜k2的正确性．请你画出图形，并简单解释．
（1）根据图2写出一个代数恒等式
2a2+3ab+b2=（2a+b）（a+b）
；（2）其实图形的面积也可以解释不等式的正确性．如已知正数a、b、c和m、n、l，并且满足a+m=b+n=c+l=k．试构造边长为k的正方形，利用其来说明al+bm+cn＜k2的正确性．请你画出图形，并简单解释．
分析：本题根据几何图形来进行代数恒等式的推导，要注意图形各部分面积和=整个图形的面积．
解答：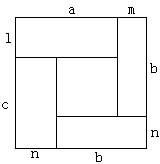
解：（1）图2的面积为：2a2+3ab+b2=图1的面积为：（2a+b）（a+b），
∴可得：2a2+3ab+b2=（2a+b）（a+b）．
（2）根据图形al+bm+cn是图中三个矩形的面积和．
而k2是正方形的面积．大小关系显而易见．
解：（1）图2的面积为：2a2+3ab+b2=图1的面积为：（2a+b）（a+b），∴可得：2a2+3ab+b2=（2a+b）（a+b）．
（2）根据图形al+bm+cn是图中三个矩形的面积和．
而k2是正方形的面积．大小关系显而易见．
点评：利用几何图形推导代数恒等式，要注意几何图形整体面积与各部分面积的关系．
练习册系列答案
相关题目
(本题6分) 我们已经知道，利用面积的不同表示方法可以写出一个代数恒等式，例如：（2a+b）（a+b）=2a2+3ab+b2，就可以用图1的图形面积的不同表示方法来表示。
（1）请写出图2所解释的代数恒等式：________________________；
（2）利用上述方法画出一个几何图形说明代数恒等式：（a+3b）（a+b）=a2+4ab+3b2的正确性。
| a2 | a2 | ab |
| ab | ab | b2 |
| ab | ab | b2 |
| a2 | a2 | ab |
| ab | ab | b2 |
解：
(本题6分) 我们已经知道，利用面积的不同表示方法可以写出一个代数恒等式，例如：（2a+b）（a+b）=2a2+3ab+b2，就可以用图1的图形面积的不同表示方法来表示。
（1）请写出图2所解释的代数恒等式：________________________；
（2）利用上述方法画出一个几何图形说明代数恒等式：（a+3b）（a+b）=a2+4ab+3b2的正确性。
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
|
ab |
ab |
b2 |
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
解：
