题目内容
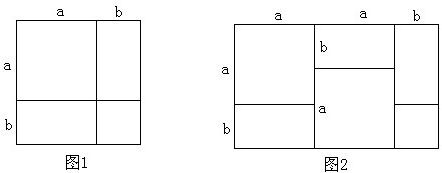
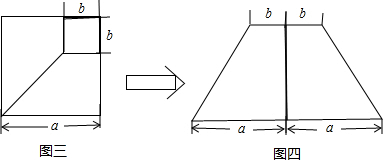
我们已经知道利用图形中面积的等量关系可以得到某些数学公式，如图一，我们可以得到两数差的完全平方公式：（a-b）2=a2-2ab+b2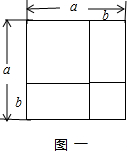
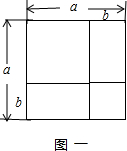
（1）请你在图二中，标上相应的字母，使其能够得到两数和的完全平方公式（a+b）2=a2+2ab+b2，
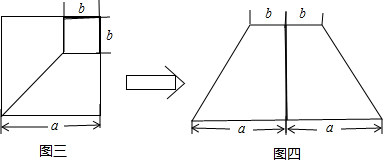
（2）图三是边长为a的正方形中剪去一个边长为b的小正方形，剩下部分拼成图四的形状，利用这两幅图形中面积的等量关系，能验证公式
（3）除了拼成图四的图形外还能拼成其他的图形能验证公式成立，请试画出一个这样的图形，并标上相应的字母．
分析：（1）此题只需将大正方形的边长表示为a，小正方形的边长表示为b即可，
（2）此题只需将两个图形的面积表示出来写成等式即可；
（3）此题还可以拼成一个矩形来验证公式的成立．
（2）此题只需将两个图形的面积表示出来写成等式即可；
（3）此题还可以拼成一个矩形来验证公式的成立．
解答：解：（1）
．
（2）根据两图形求得两图形的面积分别为：S1=a2-b2；S2=
（2a+2b）（a-b）=（a+b）（a-b）
（3）拼成的图形如下图所示：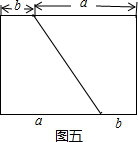
．（2）根据两图形求得两图形的面积分别为：S1=a2-b2；S2=
| 1 |
| 2 |
（3）拼成的图形如下图所示：
点评：本题考查了平方差公式及完全平方式的几何背景，考查的范围比较广．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
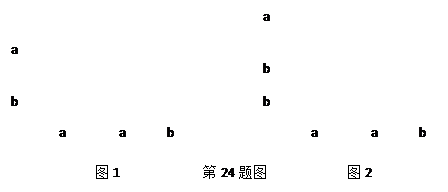
(本题6分) 我们已经知道，利用面积的不同表示方法可以写出一个代数恒等式，例如：（2a+b）（a+b）=2a2+3ab+b2，就可以用图1的图形面积的不同表示方法来表示。
（1）请写出图2所解释的代数恒等式：________________________；
（2）利用上述方法画出一个几何图形说明代数恒等式：（a+3b）（a+b）=a2+4ab+3b2的正确性。
| a2 | a2 | ab |
| ab | ab | b2 |
| ab | ab | b2 |
| a2 | a2 | ab |
| ab | ab | b2 |
解：
(本题6分) 我们已经知道，利用面积的不同表示方法可以写出一个代数恒等式，例如：（2a+b）（a+b）=2a2+3ab+b2，就可以用图1的图形面积的不同表示方法来表示。
（1）请写出图2所解释的代数恒等式：________________________；
（2）利用上述方法画出一个几何图形说明代数恒等式：（a+3b）（a+b）=a2+4ab+3b2的正确性。
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
|
ab |
ab |
b2 |
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
解：
