Question

直角三角形两直角边长分别为5和12，则它斜边上的高为________．把直角三角形的两条直角边同时扩大到原来的2倍，则其斜边扩大到原来的________ 倍．

Answer 1

    2
分析：先根据勾股定理求出斜边，设斜边上的高为x，由三角形的面积不变建立方程求出其解即可求出斜边上的高；先设出直角三角形原来的两直角边分别为a、b，就可以表示出斜边，再根据勾股定理求出扩大后的三角形的斜边就可以得出结论．
解答：由勾股定理可以求出直角边长分别为5和12的斜边为：=13，
设斜边上的高为x，由题意，得
，
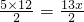解得：x=；
设原来直角三角形的两直角边分别为a、b，扩大后的直角边分别为2a、2b，由勾股定理可以求得变化前后的斜边分别为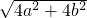；，=2，
故斜边扩大到原来的2倍．
故答案为：，2．
点评：本题考查了运用勾股定理求直角三角形的边长的运用，三角形的面积公式的运用，解答时理解勾股定理的内容是关键．