题目内容
一个几何体的主视图与左视图都是腰长为5的等腰三角形,俯视图为半径是3的圆,则这个几何体的全面积是( )A.15π
B.20π
C.24π
D.30π
【答案】分析:易得此几何体为圆锥,圆锥的全面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长,把相关数值代入即可求解.
解答:解:俯视图和主视图为等腰三角形的几何体为锥体,根据俯视图为圆可得此几何体为圆锥;
其全面积为:π×32+π×3×3=24π,
故选C.
点评:考查圆锥的全面积的计算公式,关键是根据三视图得到几何体的形状.
解答:解:俯视图和主视图为等腰三角形的几何体为锥体,根据俯视图为圆可得此几何体为圆锥;
其全面积为:π×32+π×3×3=24π,
故选C.
点评:考查圆锥的全面积的计算公式,关键是根据三视图得到几何体的形状.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
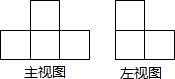 如图是一个由若干大小相同、棱长都为1的小正方体搭成一个几何体的主视图与左视图,那么下列中不一定是该几何体俯视图的是( )
如图是一个由若干大小相同、棱长都为1的小正方体搭成一个几何体的主视图与左视图,那么下列中不一定是该几何体俯视图的是( )