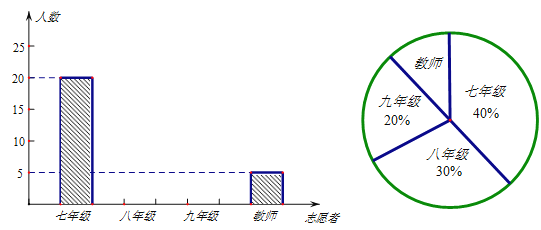
题目内容
【题目】如图，一条直线y1=klx+b与反比例函数y2= 
的图象交于A（1，5）、B（5，n）两点，与x轴交于C点， 
（1）求反比例函数的解析式；
（2）求C点坐标；
（3）请直接写出当y1＜y2时，x的取值范围．
【答案】
（1）解：∵反比例函数y2= 
的图象过点A（1，5），
∴k2=1×5=5，
∴反比例函数的解析式为y2= 
（2）解：∵反比例函数y2=⌒的图象过点B（5，n），
∴n= 
=1，
∴B（5，1）．
将A（1，5），B（5，1）代入y1=klx+b，
得 
，解得 
，
∴直线的解析式为y1=﹣x+6，
∴C点的坐标是（6，0）
（3）解：观察函数图象可知：当0＜x＜1或x＞5时，一次函数的图象在反比例函数图象的下方，
∴当y1＜y2时，x的取值范围是0＜x＜1或x＞5
【解析】（1）由A与B为一次函数与反比例函数的交点，将A坐标代入反比例函数解析式中，求出k2的值，确定出反比例解析式；（2）将B的坐标代入反比例解析式中求出n的值，确定出B的坐标，将A、B两点的坐标代入一次函数解析式中求出k1和b的值，确定出直线的解析式，进而求出C点坐标；（3）根据图象，结合交点坐标即可求解．
【题目】某超市在“元旦”促销期间规定：超市内所有商品按标价的
出售，同时当顾客在消费满一定金额后，按如下方案获得相应金额的奖券：
消费金额 |
|
|
|
获得奖券金额（元） |
|
|
|
（符号
表示
是大于或等于
，而小于
的数）
根据上述促销方法知道，顾客在超市内购物可以获得双重优惠，即顾客在超市内购物获得的优惠额
商品的折扣
相应的奖券金额，例如：购买标价为
元的商品，则消费金额为： 
元，获得的优惠额为： 
元．
（
）购买一件标价为
元的商品，求获得的优惠额．
（
）对于标价在
元与
元之间(含
元和
元)的商品，顾客购买标价为多少元的商品时可以得到
的优惠率．（设购买该商品得到的优惠率
购买商品获得的优惠额
商品的标价）
