题目内容
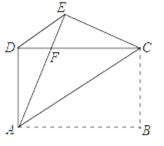
【题目】已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
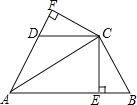
(1)BE与DF是否相等?请说明理由;
(2)若DF=1,AD=3,求AB的长;
(3)若△ABC的面积是23,△ADC面积是18,直接写出△BEC的面积.
【答案】(1)相等,理由见解析;(2)5;(3)2.5.
【解析】
(1)根据角平分线的性质可知,CF=CE,再结合已知条件利用HL证明Rt△BCE与Rt△DCF全等,最后利用全等三角形的性质解答即可;
(2)根据已知条件证明Rt△ACE≌Rt△ACF,所以AF=AE,因此AB=AE+BE=AF+BE,即可求出答案;
(3)根据(1)(2)可知,S△BCE=S△DCF,S△ACE=S△ACF,所以![]() ,即可求出答案.
,即可求出答案.
解:(1)相等,
∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,
在Rt△BCE与Rt△DCF中,![]() ,
,
∴Rt△BCE≌Rt△DCF(HL),
∴BE=DF;
(2)∵Rt△BCE≌Rt△DCF,
∴DF=EB,CE=CF,CE⊥AB于E,CF⊥AD于F,
在Rt△ACE与Rt△ACF中,![]() ,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AF=AE,
∵DF=1,AD=3,
∴AB=AF+BE=AD+DF+BE=5;
(3)∵Rt△BCE≌Rt△DCF,
∴S△BCE=S△DCF,
∵△ABC的面积是23,△ADC面积是18,
∴△BEC的面积=![]() .
.

练习册系列答案
相关题目