题目内容
如图,在□ABCD中,CE⊥AB,E为垂足,若AB=8,BC=12,则□ABCD的周长为 ;
若∠A=122°,则∠BCE的度数为 .
若∠A=122°,则∠BCE的度数为 .

40,32°
试题分析:根据平行四边形的对边相等,即可求出平行四边形的周长;再根据平行四边形的对边平行求出∠B的值,然后利用直角三角形的两个锐角互余即可求出∠BCE的度数.
∵平行四边形ABCD,
∴AD=BC=12,AB=CD=8,
∴□ABCD的周长=2(12+8)=40;
∵AD∥BC,
∴∠B=180°-∠A=58°,
又∵CE⊥AB,
∴∠BCE=32°.
点评:本题属于基础应用题,只需学生熟知平行四边形的性质,即可完成.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 中,
中, ,
, ,
, , 垂足分别为点
, 垂足分别为点 ,
, ,连接
,连接 .试问四边形
.试问四边形 是等腰梯形吗?为什么?
是等腰梯形吗?为什么?
 中,
中, 是
是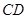 边上的中点,
边上的中点, 与
与 相交于点
相交于点 ,连接
,连接 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角). 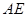 试判断
试判断 于点
于点 ,试判断
,试判断 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
