题目内容
若一元二次方程ax2+bx+c=0一个根是1,且a、b满足等式 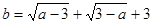 则c= .
则c= .
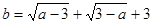 则c= .
则c= .-6
一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值,即用这个数代替未知数所得式子仍然成立;将x=1代入原方程即可求得a、b、c之间的关系,再根据已知条件即可求得c的值.
解:将x=1代入方程ax2+bx+c=0,
得:a+b+c=0;
又∵a、b满足等式b=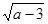 +
+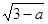 +3,
+3,
∴a-3≥0,3-a≥0;
∴a=3,
∴b=3;
则c=-a-b=-6.
本题需注意当函数表达式是二次根式时,被开方数为非负数.
解:将x=1代入方程ax2+bx+c=0,
得:a+b+c=0;
又∵a、b满足等式b=
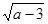 +
+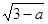 +3,
+3,∴a-3≥0,3-a≥0;
∴a=3,
∴b=3;
则c=-a-b=-6.
本题需注意当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
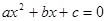 的两个根是-3和1,那么二次函数
的两个根是-3和1,那么二次函数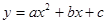 的图象的对称轴是直线( ).
的图象的对称轴是直线( ).  =-3
=-3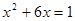
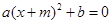 的解是x1=-2,x2=1(a,m,b均为常数,a≠0),则方程
的解是x1=-2,x2=1(a,m,b均为常数,a≠0),则方程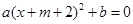 的解是 .
的解是 .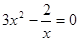
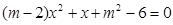 的一个根为2,则m为( )
的一个根为2,则m为( )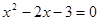 (考查一元二次方程的解法)
(考查一元二次方程的解法)
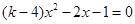 。
。