题目内容
已知直线m的解析式为y=-
x+4,与x轴、y轴分别交于A、B两点,以线段AB为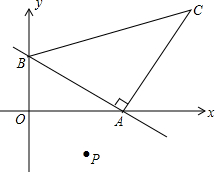 直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.
直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.
(1)求A,B两点的坐标;
(2)求△ABC的面积;
(3)求a的值.
| ||
| 3 |
 直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.
直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.(1)求A,B两点的坐标;
(2)求△ABC的面积;
(3)求a的值.
分析:(1)先令y=0求出x的值,再令x=0求出y的值即可得出A、B两点的坐标;
(2)先根据AB两点的坐标求出OA、OB的值,再由勾股定理求出AB的长度,根据三角形的面积公式即可得出△ABC的面积;
(3)当点P在第一象限时,过点P作PD⊥x轴,此时OD=OA+AD=a,PD=2,由于△ABP的面积与△ABC的面积相等,故S△ABP=S梯形ODPB-S△AOB-S△APD=32,故可求出a的值;
当点P在第二象限时,连接OP,过点P作PE⊥x轴,由△ABP的面积与△ABC的面积相等,可知S△ABP=S△POB+S△AOB-S△AOP=32,故可得出a的值.
(2)先根据AB两点的坐标求出OA、OB的值,再由勾股定理求出AB的长度,根据三角形的面积公式即可得出△ABC的面积;
(3)当点P在第一象限时,过点P作PD⊥x轴,此时OD=OA+AD=a,PD=2,由于△ABP的面积与△ABC的面积相等,故S△ABP=S梯形ODPB-S△AOB-S△APD=32,故可求出a的值;
当点P在第二象限时,连接OP,过点P作PE⊥x轴,由△ABP的面积与△ABC的面积相等,可知S△ABP=S△POB+S△AOB-S△AOP=32,故可得出a的值.
解答:解:(1)∵令y=0,则x=4
,
x=0,则y=4,
∴A(4
,0),B(0,4);
(2)∵A(4
,0),B(0,4),
∴OA=4
,OB=4,
∴AB=
=
=8,
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AB=AC=8,
∴S△ABC=
AB•AC=
×8×8=32;

(3)∵点P(a,2),
∴点P在第一象限或第二象限,
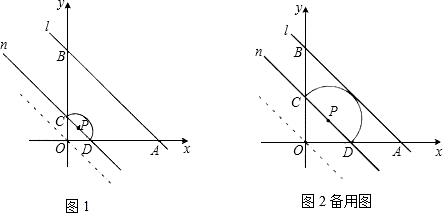
当点P在第一象限时,如图1所示,
过点P作PD⊥x轴,此时OD=OA+AD=a,PD=2,
∵△ABP的面积与△ABC的面积相等,
∴S△ABP=S梯形ODPB-S△AOB-S△APD=
(2+4)×a-
×4×4
-
×2×(a-4
)=32,
解得a=16+2
;
当点P在第二象限时,如图2所示:
连接OP,过点P作PE⊥x轴,
此时AE=4
-a,
∵△ABP的面积与△ABC的面积相等,
∴S△ABP=S△POB+S△AOB-S△AOP=
OB•OE+
OB•OA-
OA•PE=
×4×(-a)+
×4×4
-
×4
×2=32,
解得a=-16+2
.
综上所述a的值为a1=16+2
,a2=-16+2
.
| 3 |
x=0,则y=4,
∴A(4
| 3 |
(2)∵A(4
| 3 |
∴OA=4
| 3 |
∴AB=
| OA2+OB2 |
(4
|
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AB=AC=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |

(3)∵点P(a,2),
∴点P在第一象限或第二象限,
当点P在第一象限时,如图1所示,
过点P作PD⊥x轴,此时OD=OA+AD=a,PD=2,
∵△ABP的面积与△ABC的面积相等,
∴S△ABP=S梯形ODPB-S△AOB-S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
解得a=16+2
| 3 |
当点P在第二象限时,如图2所示:
连接OP,过点P作PE⊥x轴,
此时AE=4
| 3 |
∵△ABP的面积与△ABC的面积相等,
∴S△ABP=S△POB+S△AOB-S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
解得a=-16+2
| 3 |
综上所述a的值为a1=16+2
| 3 |
| 3 |
点评:本题考查的是一次函数综合题,涉及到勾股定理、梯形的面积公式及三角形的面积公式,在解答(3)时要注意分类讨论,不要漏解.

练习册系列答案
相关题目
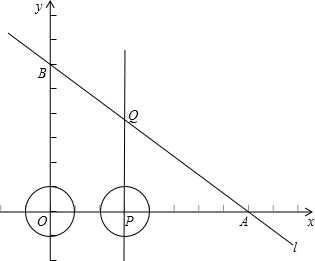 轴分别交于点A、B.
轴分别交于点A、B.
 如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=-
如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=-