题目内容
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形 的边
的边 恰好被点
恰好被点 平分,边
平分,边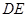 交双曲线于
交双曲线于 点,四边形
点,四边形 的面积为2.
的面积为2.

(1)求n的值;
(2)求不等式 的解集
的解集
 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形 的边
的边 恰好被点
恰好被点 平分,边
平分,边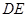 交双曲线于
交双曲线于 点,四边形
点,四边形 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式
 的解集
的解集(1) ;(2)
;(2) 的解集为
的解集为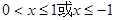 .
.
 ;(2)
;(2) 的解集为
的解集为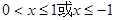 .
.试题分析:(1)先根据矩形性质和线段中点的坐标公式得到D(2b,﹣2),则矩形OCDE的面积=4b,再根据反比例函数的比例系数的几何意义得到S△OCB=S△OEF=
 |n|=﹣
|n|=﹣ n,然后利用四边形OBDF的面积=矩形OCDB﹣S△OCB﹣S△OEF,可求出n;
n,然后利用四边形OBDF的面积=矩形OCDB﹣S△OCB﹣S△OEF,可求出n;(2)由于反比例解析式为y=﹣
 ,则B点坐标为(1,﹣2),再利用反比例函数的性质确定A点坐标为(﹣1,2),然后观察函数图象求解.
,则B点坐标为(1,﹣2),再利用反比例函数的性质确定A点坐标为(﹣1,2),然后观察函数图象求解.试题解析:(1)连接
 .
.
∵边
 恰好被点
恰好被点 平分,
平分, ∴
 ,
,∵矩形
 ,
,∴

∵
 ,
,∴

∴
 ,
,∵双曲线分布在二、四象限,
∴
 ;
;(2)把
 代入
代入 ,得
,得 ,
,∴
 点的横坐标为1.
点的横坐标为1.∵双曲线及过原点的直线均是关于原点成中心对称的图形
∴它们的交点也关于原点成中心对称,
∴
 点的横坐标为
点的横坐标为 ,
,由图像可知:
 的解集为
的解集为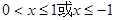 .
.
练习册系列答案
相关题目





 或
或 .
.
 (
( )的函数值
)的函数值 随
随 的增大而增大,则一次函数
的增大而增大,则一次函数 的图象大致是( )
的图象大致是( )
 和
和 有相等的函数值,则
有相等的函数值,则 的值为( )
的值为( )

