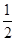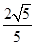题目内容
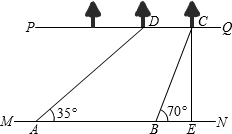
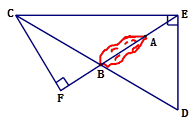
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE.(结果保留两个有效数字)(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70, Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

66米.
试题分析:过点C作CF∥DA交AB于点F,易证四边形AFCD是平行四边形.再在直角△BEC中,利用三角函数求解.
过点C作CF∥DA交AB于点F.
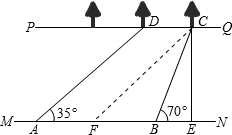
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB-AF=120-50=70m.
根据三角形外角性质可知,∠CBN=∠CFB+∠BCF,
∴∠BCF=70°-35°=35°=∠CFB,
∴BC=BF=70m.
在Rt△BEC中,
sin70°=
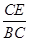 ,
,∴CE=BC•sin70°≈70×0.94=65.8≈66m.
答:河流的宽是66米.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45
方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45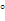 方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)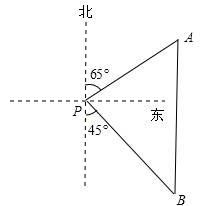

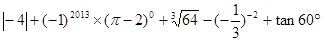
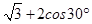 的值为 .
的值为 .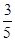 .
.
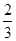 小时到达B处,那么tan∠ABP=( )
小时到达B处,那么tan∠ABP=( )