题目内容
 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.试探索CF与DE的位置关系,并说明理由.
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.试探索CF与DE的位置关系,并说明理由.
解:CF⊥DE,CF平分DE,理由是:
∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
 ,
,
∴△ACD≌△BEC(SAS),
∴DC=CE,
∵CF平分∠DCE,
∴CF⊥DE,CF平分DE(三线合一).
分析:根据平行线性质得出∠A=∠B,根据SAS证△ACD≌△BEC,推出DC=CE,根据等腰三角形的三线合一定理推出即可.
点评:本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质等知识点,关键是求出DC=CE,主要考查了学生运用定理进行推理的能力.
∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
 ,
,∴△ACD≌△BEC(SAS),
∴DC=CE,
∵CF平分∠DCE,
∴CF⊥DE,CF平分DE(三线合一).
分析:根据平行线性质得出∠A=∠B,根据SAS证△ACD≌△BEC,推出DC=CE,根据等腰三角形的三线合一定理推出即可.
点评:本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质等知识点,关键是求出DC=CE,主要考查了学生运用定理进行推理的能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

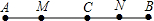
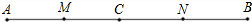
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长; 如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=
如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=