题目内容
如图，将一个长为a，宽为b的长方形沿虚线剪开，拼接成为一个缺角（也是一个小正方形）的大正方形，则缺少的这个小正方形的边长为
- A.
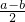
- B.a-b
- C.
- D.
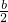
A
分析：设去掉的小正方形的边长为x，根据题意可得等量关系：大正方形的面积=原长方形的面积+小正方形的面积．特别注意剪拼前后的图形面积相等．
解答：
解：设去掉的小正方形的边长为x，
则：（b+x）2=ab+x2，
解得：x=，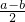
故选：A．
点评：此题主要考查了一元一次方程的应用，解决此类问题一定要联系方程根据图形的面积来解决．
分析：设去掉的小正方形的边长为x，根据题意可得等量关系：大正方形的面积=原长方形的面积+小正方形的面积．特别注意剪拼前后的图形面积相等．
解答：
解：设去掉的小正方形的边长为x，则：（b+x）2=ab+x2，
解得：x=
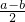，故选：A．
点评：此题主要考查了一元一次方程的应用，解决此类问题一定要联系方程根据图形的面积来解决．
练习册系列答案
相关题目
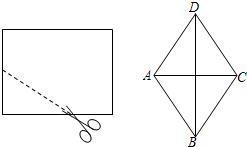如图，将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）| A、10cm2 | B、20cm2 | C、40cm2 | D、80cm2 |
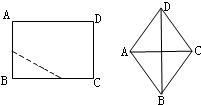
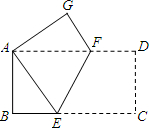如图，将一个长为8cm，宽为4cm的长方形纸片ABCD折叠，使C点与A点重合，求GF的长．
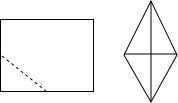如图，将一个长为20cm，宽为16cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）
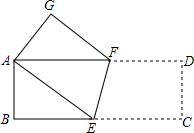如图，将一个长为9，宽为3的长方形纸片ABCD延EF折叠，使点C与点A重合，则EF的长为